图算法
算法列表
路径搜索算法
图搜索算法是用于在图中探索大量路径的算法,主要用于广泛的搜索或显式搜索。这些算法包括广度优先搜索和深度优先搜索,可以遍历图中的大量路径,但并不总是期望找到计算最优的路径(例如最短或权重最小),通常是许多其他类型分析的第一步。
路径搜索算法建立在图搜索算法的基础上,探索各点之间的路径。这些算法识别最优路径,主要用于物流规划、最低成本呼叫或 IP 路由问题以及游戏模拟等。
| 英文名称 | 中文名称 | 算法说明 | 应用场景 |
|---|---|---|---|
| Average_Shortest_Path_Length | 平均最短路径长度 | 计算图中两个点之间的平均最短路径长度。 | 路径设计、网络规划等 |
| Shortest_Path | 最短路径 | 在图中查询一个起始点到终点之间的所有最短路径。 | 路径规划、导航等 |
| BFS | 多跳算法 | 返回图中其他点到起点的多跳值。 | 搜索、路由协议等 |
| SSSP(Single-Source Shortest Path) | 单源最短路径 | 计算在图中起点到其他所有点的最短距离。 | 网络路由、路径设计等 |
| MSSP | 多源最短路径 | 从多个起点出发,计算到达任意点的最短路径长度。任意点的最短路径长度是从所有起点到达该点的最短路径中的最小值。 | 物流优化、网络路由等 |
| KSSSP | k 步最短路径 | 计算图上 k 跳以内的最短路径长度。 | 网络路由、路径规划等 |
| SSSP_Has_Path | 路径存在判断 | 判断两点之间是否存在路径。 | 图查询、路由协议等 |
| Is_Simple_Path | 简单路径判定 | 判断给定的一组点是否能组成一条简单路径。 | 图查询、路径规划等 |
| All_Path_Search | 全路径搜索 | 在图中查找两点间 K 跳以内的所有路径。 | 路由协议、网络分析等 |
| Random_Walk | 随机游走 | 随机游走算法是一种基于概率的图遍历算法,它模拟在图或网络中的随机移动过程。该算法从一个起点开始,按照一定的概率选择下一个点,并重复该过程,直到满足停止条件。 | 链接预测等 |
| Diameter | 直径估计算法 | 直径估计算法是一种用于估计图的直径的算法。图的直径是指图中任意两个点之间最短路径的最大长度,是描述图大小和连接性的重要指标之一。 | 图分析、网络优化等 |
| Node_Boundary | 点边界 | 在图中点边界为图内两个子图 T 和 S 的边界点集合,集合内每个点都在 T 中,且存在一条边连接到 S 中的点。 | 社交网络、关系网络等 |
| Edge_Boundary | 边边界 | 边界边是指连接着两个不同社区的边。边界边算法是指一种用于识别边界边的算法,其主要目的是确定社区之间的边界,并促进不同社区之间的联系和信息传递。 | 社交网络、关系网络、Web 网页链接分析等 |
| All_Shortest_Path | 节点对最短路径 | 查询图中两点之间的最短路径。 | 图分析、网络优化等 |
| All_Simple_Paths | 所有简单路径 | 查询一个起点经过给定点的所有简单路径。 | 路径规划、组合优化等 |
| SSSP_All_Pairs_Length | 所有点对最短路径长度 | 计算图中所有点之间的最短路径长度。 | 图分析、网络优化等 |
| DFS | 深度优先搜索 | 通过深度优先搜索算法查找各个点到起点的距离。 | 网络路由、搜索引擎的爬虫、信息检索等。 |
| Multi_Source_Khop | 多源多跳 | 支持根据实际情况查找多个起点 K 跳的结果,支持返回 K 跳的点或者 k 跳的点的数量。 | 网络路由、搜索引擎的爬虫、信息检索等。 |
| BFS_Generic | 通用广度优先搜索 | 是一种广泛使用的图搜索算法,用于在图中查找从源点到目标点的最短路径或最少步数。BFS 采用队列数据结构,按照广度优先的顺序遍历图中的点。 | 网络路由、搜索引擎的爬虫、信息检索等。 |
中心性算法
中心性算法(Centrality Algorithms)用于识别图中特定点的角色及其对网络的影响。中心性算法能够帮助识别最重要的点,帮助了解组动态,例如可信度、可访问性、事物传播的速度以及组与组之间的连接。尽管这些算法中有许多是为社会网络分析而发明的,但它们已经在许多行业和领域中得到了应用。
中心度分析算法�
| 英文名称 | 中文名称 | 算法说明 | 应用场景 |
|---|---|---|---|
| Degree_Centrality | 度中心性 | 计算图中每一个点的归一化度数。一个点的度(数)越大,则该点的度中心性越高,就说明在图中这个点越重要。 | 社会网络分析、网络用户行为分析等 |
| Eigenvector_Centrality | 特征向量中心度 | 用来度量各点之间的传递影响和连通性,在特征向量中心度算法中,点与具有高得分的点相连接比与具有低得分的点相连接所得的贡献更大。 | 网络排名、社交网络分析等 |
| Katz_Centrality | Katz 中心性 | Katz 中心性算法通过测量相邻点和网络中通过这些相邻点连接到该点的其他所有点的数量,计算网络中点的相对影响。 | 网络分析、推荐系统等 |
| Voterank | 投票排名算法 | 基于投票方案计算图中点的排名。 | 社交网络分析、图像分割等 |
| Closeness_Centrality | 紧密中心度 | 紧密中心度是一种衡量点在图中的中心性的指标,用于衡量点与其他点之间的接近程度。 | 监控资源流动、信息传播等 |
| Betweenness_Centrality | 介数中心度 | 介数中心度是一种衡量网络中点重要性的指标,它反映了点在网络中连接其他点的重要性。介数中心度的值越高,表示该点在网络中的中介地位越重要。 | 优化交通路线、改善交通流动性、设计公共交通系统等 |
| Edge_Betweenness_Centrality | 边介数中心度 | 是一种用于衡量网络中边重要性的指标。衡量边在网络中作为桥梁的程度,即边在连接点之间的重要性。边介数中心度的值越高,表示该边在网络中作为连接路径的重要性越大。 | 网络分析、社交网络研究等 |
影响力分析算法
影响力分析算法是一种在图计算中衡量图中点或边的影响力的算法。这种算法通常用于社交网络分析、推荐系统、传染病传播等领域。
| 英文名称 | 中文名称 | 算法说明 | 应用场景 |
|---|---|---|---|
| Pagerank | 网页排名 | PageRank 是一种基于图的排序算法,用于在网页之间进行排名。通过给每个网页中每个点附加权值,对点的重要性进行排序。 | 社交网络重点人物发掘、网页排序等 |
| Weight_Pagerank | 加权网页排名 | 加权网页排名是对 PageRank 算法的一种扩展,Rank 值的传递跟边的权重有关,点的 Rank 值将按照边权重加权传递到相邻点。 | 搜索引擎、网页排序等 |
| Sybil_Rank | sybil 指数 | sybil 指数算法可用于垃圾节点检测, sybilrank 是通过提前终止的随机游走对网络中各点的可信度进行排名的算法。 | 在线社交网络等 |
| HITS | 链接分析 | HITS(Hyperlink-Induced Topic Search,基于超链接的主题搜索) 是一种在图上对点进行评级的算法。 | 搜索引擎、链接分析等 |
社区发现算法
社区的形成在各种类型的网络中都很常见。识别社区对于评估群体行为或突发事件至关重要。对于一个社区来说,内部点与内部点的边比社区外部点的边更多。识别这些社区可以揭示点的分区,找到孤立的社区,发现整体网络结构关系。社区发现算法有助于发现社区中群体行为或者偏好,寻找嵌套关系,或者成为其他分析的前序步骤。社区发现算法也常用于网络可视化场景。
度量算法
在图计算中,度量算法用于衡量图中点或边之间相似性或关联程度的一种算法,主要包含三角计数、聚类系数、平均聚类系数、传递性等算法等。
| 英文名称 | 中文名称 | 算法说明 | 应用场景 |
|---|---|---|---|
| Triangles | 三角计数 | 计算图中每个点的三角形数量,一个图中有很多三角形,说明该社区很稳定,各点间的联系比较紧密。 | 衡量图的结构特性场景等 |
| Clustering | 聚类系数 | 计算图中每个点的聚类系数,它反映了与该点相关联的点彼此有关联的概率。 | 衡量图的结构特性场景等 |
| Avg_Clustering | 平均聚类系数 | 计算所有点聚类系数的平均值。 | 网络分析、社交网络研究等 |
| Transitivity | 传递性 | 传递性用来衡量相邻点共享相同的邻居点的比例。 | 网络分析、社交网络研究等 |
连通性算法
连通性算法是一种在图计算中判断图的连通性的算法。主要包括弱连通分量、弱连通分量数和强连通分量等算法。这些算法广泛应用于社交网络分析、网络路由优化、图像分割等多个领域。例如,在社交网络分析中,利用连通性算法可以检测到社群之间的连通性,从而分析社会关系;在网络路由优化中,通过分析网络的拓扑结构,可以快速且可靠地传输数据;在图像分割中,连通性算法可用于判断图像中的连通区域,从而提取出目标。连通性算法是一种重要的图计算算法,具有广泛的应用前景。
| 英文名称 | 中文名称 | 算法说明 | 应用场景 |
|---|---|---|---|
| WCC | 弱连通分量 | 在无向图中,弱连通分量是原始图的一个子图,其中,忽略边的方向,所有的点都通过某种路径相互连接。 | 网络分析、社交网络研究等 |
| Number_Connected_Components | 弱连通分量数 | 在无向图中,返回弱连通分量子图个数。 | 网络分析、社交网络研究等 |
| SCC | 强连通分量 | 在有向图中,强连通分量是原始图的一个子图,其中,所有的点通过某种路径都相互可达。 | 网络分析、社交网络研究等 |
标签传播算法
LPA(Label Propagation Algorithm)是一种社区检测算法,它的核心思想是社区内部点标签的传播。该算法可以自动将具有相似特征的点聚类到一起,形成一个社区。LPA 算法的实现过程中,将每个点随机初始化为一个标签,然后在每一轮迭代中,点将自己的标签更新为其邻居点中出现最频繁的标签。在 LPA 算法的迭代过程中,每个点都会不断地接收来自邻居点的标签信息,并不断地调整自己的标签,直到收敛为止。最终,具有相同标签的点构成一个社区。
LPA 算法可以应用于许多领域,例如社交网络分析和生物信息学。在社交网络中,LPA 算法可以帮助我们识别出具有相似兴趣爱好或社交关系的用户,并将他们划分到同一社区中。在生物信息学中,LPA算法可以识别出同一基因家族的基因,并将它们划分到同一簇中。LPA算法的优势在于简单易懂,迭代速度快,对于大规模数据集的处理效果尤为明显。
| 英文名称 | 中文名称 | 算法说明 | 应用场景 |
|---|---|---|---|
| LPA(Label Propagation Algorithm)、LPA_U2I | 标签传播算法 | LPA 是一种社区检测算法,主要是用于社区内部点标签的传播。该算法可以自动将具有相似特征的点聚类到一起,形成一个社区。其中,标签传播(LPA_U2I)为一种特殊图场景的实现,仅支持在只有一种边边类型和两种点类型的图中使用。 | 社交网络分析、生物信息学等 |
| WCDLP | 加权标签传播 | 基于标签传播算法,加权标签传播与边的权重相关,在标签传播时,每个点根据标签的入边情况进行权重累加,并在累加权重或最高的标签中随机选择一个。 | 图聚类、社区发现等 |
| SLPA | 监听标签传播 | 监听标签传播算法是基于标签传播和历史标签记录的社区发现算法,是对标签传播算法的扩展。该算法记录所有点的历史标签,并在迭代中累加标签时考虑历史标签。最终输出每个点的所有历史标签记录。 | 社区发现等 |
社区检测算法
社区检测算法基于图论和网络分析的方法来发现网络中的社区结构,是一种网络聚类的方法,用于揭示网络中��的聚集行为。它可以识别网络中的社区结构,即一组紧密连接的点,它们之间连接紧密,而与其他社区的连接则相对稀疏。
| 英文名称 | 中文名称 | 算法说明 | 应用场景 |
|---|---|---|---|
| Louvain | 鲁汶社区 | 鲁汶算法是基于模块度的社区发现算法,能够发现层次性的社区结构,并最大化整个社区网络的模块度。 | 社交网络分析、网络聚类、社区发现等 |
| Girvan-Newman(gn) | Girvan-Newman 算法(gn) | GN 图算法是一种用于社区发现的图分析算法,主要目标是识别复杂网络中的社区结构,同时最大化社区内的连接密度,最小化社区之间的连接密度。 | 社交网络分析、网络聚类、社区发现等 |
关联性分析
关联性分析算法用于研究点之间的关联性、相似性以及连接模式。在多个领域中有广泛的应用,主要应用场景如下:
- 关联性分析算法可用于研究社交网络中的点关系、群体聚集和信息传播等,通过分析点相似度和同配性等指标,可以揭示社交网络中的社区结构、影响力点和信息传播路径。
- 关联性分析算法可用于推荐系统中的相似性匹配和链接预测。通过分析用户的行为模式和物品的关联关系,可以�推断用户的兴趣并提供个性化的推荐结果。
- 关联性分析算法可用于研究金融市场中的点关联和系统风险。通过分析金融机构之间的关联关系和同配性,可以预测系统性风险传播路径和评估金融市场的稳定性。
同配性算法
用于分析点连接与点属性或度之间的相关性。
| 英文名称 | 中文名称 | 算法说明 | 应用场景 |
|---|---|---|---|
| Degree Assortativity Coefficient | 度同配系数 | 度同配系数算法是一种衡量图中点的度相关性的算法 | 网络分析、社交网络研究等 |
| Average Degree Connectivity | 平均相邻度算法 | 平均相邻度算法是计算图的平均度连接性的算法。 | 社区发现、网络中心性分析等 |
点相似度算法
用于计算点之间的相似性指标,以衡量它们在图中的关联程度。
| 英文名称 | 中文名称 | 算法说明 | 应用场景 |
|---|---|---|---|
| Vertex_Similarity_SS | 单源点相似度 | 给定起点,返回 top k 内相似度的点及相似值,支持 jaccard 系数和 Common 两种相似度计算方法。 | 图聚类、推荐系统等 |
| Vertex_Similarity | 点相似度 | 判断两组点之间各个点的相似度。 | 图聚类、推荐系统等 |
子图挖掘算法
图挖掘(Graph Mining)是利用图模型从大量数据中发现、提取有用知识和信息的过程。所获得的知识和信息已广泛应用于商务管理、市场分析、生产控制、科学探索和工程设计等领域。
| 英文名称 | 中文名称 | 算法说明 | 应用场景 |
|---|---|---|---|
| K_Core | k 核算法 | k 核算法主要用于计算每个点的核数(度数)。 | 图推演、生物学、社交网络、金融风控等 |
| K_Shell | k 壳算法 | k 壳算法是一种图结构分析算法,递归的剥离图中度数小于或等于 k 的点,直到图中所有的点都被赋予 ks 值为止。 | 网络分析、社区发现、网络演化等 |
| Graph_Matching | 图模式匹配 | 图模式匹配算法是指在一个大型图中查找并自动识别模式图,并从中提取出关键信息的算法。 | 神经科学、仿生学、社交网络和关系数据挖掘等 |
| Cycle_Detection | 环路检测 | 环路检测是一种图分析算法,用于在图中找到所有 K 跳以内的环路。 | 网络分析、交通路网分析等 |
| Ego_Net | EgoNet 算法 | EgoNet 算法是一种基于根顶点的子图挖掘算法,它的目标是找到根顶点周围的邻居点,并以根顶点为中心构建一个包含根顶点及其 K 度以内邻居点的子图,该子图被称为根顶点的 EgoNet。 | 社交网络分析、网络构建等 |
平均最短路径长度(average_shortest_path_length)
概述
计算图中两个节点对之间的平均最短路径长度��。适用于路径设计、网络规划等场景。
语法
MATCH ... CALL average_shortest_path_length((n)-[e]->(b))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| weight | Property | 否 | 权重属性 | e.weight |
结果输出
| 名称 | 描述 |
|---|---|
| result | 平均最短路径长度 |
示例
-
查询语句
MATCH (n:person)-[e:likes]->(b:post) call average_shortest_path_length((n)-[e]->(b), e.weight)
YIELD task_id
RETURN task_id; -
期望结果
+----------------------+
| 0 |
+======================+
| 0.048214285714285716 |
+----------------------+
最短路径(shortest_path)
概述
查询一个起点到一个终点的所有最短路径。 在图中查询一个起始点到目标点之间的最短路径。
语法
MATCH ... CALL shortest_path((n)-[e]->(b), $(source), $(target), $(k), $(directed),$(weight), $(weight property))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| sourcce | int | 否 | 起始点, 格式为 点类型:点id | 36152353956560896 | ||
| target | int | 否 | 起始点, 格式为 点类型:点id | 36152353956560900 | ||
| k | int | 否 | 最大跳数 | 3 | ||
| directed | int | 否 | 边方向 0:out, 1:in , 2:both | 2 | ||
| weight | str | 否 | 权重属性名字 | "weight" | ||
| property | Property | 否 | 权重属性 | e.weight |
结果输出
| 名称 | 描述 |
|---|---|
| id | 最短路径 |
示例
- 查询语句
MATCH (n:person)-[e:knows]->(b:person) call shortest_path((n)-[e]->(b),36152353956560896,36152353956560903,"weight",e.weight)
YIELD task_id
RETURN task_id; - 期望结果
+--------------------+----------+---------+---+-------------------+-----------+
| 0 | | | | | |
+====================+==========+=========+===+===================+===========+
| [36152353956560900 | "person" | "knows" | 0 | 36152353956560903 | "person"] |
+--------------------+----------+---------+---+-------------------+-----------+
| [36152353956560897 | "person" | "knows" | 0 | 36152353956560900 | "person"] |
+--------------------+----------+---------+---+-------------------+-----------+
| [36152353956560896 | "person" | "knows" | 0 | 36152353956560897 | "person"] |
+--------------------+----------+---------+---+-------------------+-----------+
多跳算法(BFS)
概述
返回图中其他点到目标点的多跳值。
语法
MATCH ... call bfs($(path), $(src))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| src | int | 否 | 起始点, 格式为 点类型:点id | 36152353956560896 |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点 ID |
| result | 与起始点的距离 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call bfs((n)-[e]->(b), 36152353956560896)
YIELD task_id
RETURN task_id; - 期望结果
+--------------------+---------------------+
| id | result |
+====================+=====================+
| 36152353956560897 | 9223372036854775807 |
+--------------------+---------------------+
| 36152353956560896 | 0 |
+--------------------+---------------------+
| 36152353956560898 | 9223372036854775807 |
+--------------------+---------------------+
| 36152353956560906 | 9223372036854775807 |
+--------------------+---------------------+
| 36152353956560907 | 9223372036854775807 |
+--------------------+---------------------+
| 108209947994488859 | 1 |
+--------------------+---------------------+
| 108209947994488860 | 1 |
+--------------------+---------------------+
| 108209947994488858 | 9223372036854775807 |
+--------------------+---------------------+
*9223372036854775807 类似这样的数字表示∞,点不可达
单源最短路径(sssp)
概述
计算图上的单源最短路径长度。给定图中一个顶点,计算给定顶点到其他所有点的最短距离。适用于网络路由、路径设计等场景。
语法
MATCH ... call sssp($(path), $(src), $(weight))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| src | int | 否 | 起始点, 格式为 点类型:点id | 36152353956560896 | ||
| weight | Property | 否 | 权重字段 | e.weight |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点 ID |
| result | 顶点及 src 到其的最短距离 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call sssp((n)-[e]->(b),36152353956560896, e.weight)
YIELD task_id
RETURN task_id; - 期望结果
+--------------------+-------------------------+
| id | result |
+====================+=========================+
| 36152353956560897 | 1.7976931348623157e+308 |
+--------------------+-------------------------+
| 36152353956560896 | 0.0 |
+--------------------+-------------------------+
| 36152353956560898 | 1.7976931348623157e+308 |
+--------------------+-------------------------+
| 36152353956560906 | 1.7976931348623157e+308 |
+--------------------+-------------------------+
| 36152353956560907 | 1.7976931348623157e+308 |
+--------------------+-------------------------+
| 108209947994488859 | 0.1 |
+--------------------+-------------------------+
| 108209947994488860 | 0.6 |
+--------------------+-------------------------+
| 108209947994488858 | 1.7976931348623157e+308 |
+--------------------+-------------------------+
多源最短路径(mssp)
概述
根据给定的多个源顶点,从这些源顶点出发,计算到达任意顶点的最短路径值。其中,多个源顶点到某一顶点的最短路径值为分别从每个源顶点出发到达该顶点的最短路径的最小值。
语法
MATCH ... CALL mssp($(path),$(source), $(weight), $(weight_) )
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| source | List | 否 | 源顶点列表 | '[36152353956560896]' | ||
| weight | str | 否 | 权重属性名 | "weight" | ||
| weight_ | Property | 否 | 权重属性 | e.weight |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点oid |
| result | 平均最短路径长度 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call mssp((n)-[e]->(b), '[36152353956560896]', "weight",e.weight)
YIELD task_id
RETURN task_id;
- 期望结果
+--------------------+-------------------------+
| id | result |
+====================+=========================+
| 36152353956560897 | 1.7976931348623157e+308 |
+--------------------+-------------------------+
| 36152353956560896 | 0.0 |
+--------------------+-------------------------+
| 36152353956560898 | 1.7976931348623157e+308 |
+--------------------+-------------------------+
| 36152353956560906 | 1.7976931348623157e+308 |
+--------------------+-------------------------+
| 36152353956560907 | 1.7976931348623157e+308 |
+--------------------+-------------------------+
| 108209947994488859 | 0.1 |
+--------------------+-------------------------+
| 108209947994488860 | 0.6 |
+--------------------+-------------------------+
| 108209947994488858 | 1.7976931348623157e+308 |
+--------------------+-------------------------+
k步最短路径(ksssp)
概述
计算图上的k跳以内的最短路径长度。给定图中一个顶点,计算给定顶点到其他所有点的最短距离。适用于网络路由、路径设计等场景。
语法
MATCH ... CALL ksssp($(path),$(src),$(k),$(weight_) )
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| src | List | 否 | 源顶点ID列表 | '[36152353956560896,36152353956560897]' | ||
| k | int | 否 | 跳数 | |||
| weight_ | Property | 否 | 权重属性 | e.weight |
结果输出
| 名称 | 描述 |
|---|---|
| result | 平均最短路径长度 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call ksssp((n)-[e]->(b),'[36152353956560896, 36152353956560897]', 3, e.weight)
YIELD task_id
RETURN task_id; - 期望结果
+--------------------+-------------------------+
| id | result |
+====================+=========================+
| 36152353956560897 | 1.7976931348623157e+308 |
+--------------------+-------------------------+
| 36152353956560896 | 1.7976931348623157e+308 |
+--------------------+-------------------------+
| 36152353956560898 | 1.7976931348623157e+308 |
+--------------------+-------------------------+
| 36152353956560906 | 1.7976931348623157e+308 |
+--------------------+-------------------------+
| 36152353956560907 | 1.7976931348623157e+308 |
+--------------------+-------------------------+
| 108209947994488859 | 1.7976931348623157e+308 |
+--------------------+-------------------------+
| 108209947994488860 | 1.7976931348623157e+308 |
+--------------------+-------------------------+
| 108209947994488858 | 1.7976931348623157e+308 |
+--------------------+-------------------------+
路径存在判断(sssp_has_path)
概述
检查给定两点之间是否存在路径。
语法
MATCH ... CALL sssp_has_path($(path), $(src), $(dst))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| src | str | 否 | 起始点, 格式为 点类型:点id | "person:psn1" | ||
| dst | str | 否 | 终点, 格式为 点类型:点id | "post:pst1" |
结果输出
| 名称 | 描述 |
|---|---|
| 0 | 是否有最短路径 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call sssp_has_path((n)-[e]->(b), "person:psn1", "post:pst2")
YIELD task_id
RETURN task_id; - 期望结果
+------+
| 0 |
+======+
| True |
+------+
简单路径判定(is_simple_path)
概述
查询一组点是否是组成一条简单路径。
语法
MATCH (n:person)-[e:knows]->(b:person) call is_simple_path((n)-[e]->(b), $(nodes))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| nodes | list | 否 | 点列表 | '[36152353956560896,108209947994488859]' |
结果输出
| 名称 | 描述 |
|---|---|
| 0 | 是否是简单路径 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call is_simple_path((n)-[e]->(b), '[36152353956560896,108209947994488859]')
YIELD task_id
RETURN task_id; - 期望结果
+------+
| 0 |
+======+
| True |
+------+
全路径搜索(all_path_search)
概述
给定两个节点序列,返回k跳以内的两个节点集的全部路径,在社交网络或复杂网络中,可以用于发现不同社区之间的关联路径,帮助揭示网络的社区结构和社区之间的连接,在生物学中,多源路径搜索可以用于分析基因调控网络中不同基因集群之间的路径,以揭示基因之间的调控关系和信号传递路径。
HTAP 语法
MATCH ... call all_path_search($(path), $(nodes), $(nodes2), $(k))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| nodes1 | List | 否 | 顶点列表1 | '[36152353956560896]' | ||
| nodes2 | List | 否 | 顶点列表2 | '[36152353956560906,36152353956560900]' | ||
| k | int | 否 | 最大跳数 | 3 |
结果输出
| 名称 | 描述 | 返回格式 |
|---|---|---|
| 0 | 路径序列(集合) | 集合的方式 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call all_path_search((n)-[e]->(b), '[36152353956560906]', '[108209947994488858,108209947994488859,108209947994488860,108209947994488861]', 3)
YIELD task_id
RETURN task_id; - 期望结果
+-----------+----------------------------+---------+---+----------+-----------------------------+
| 0 | | | | | |
+===========+============================+=========+===+==========+=============================+
| ["person" | "person:36152353956560906" | "likes" | 0 | "post" | "post:108209947994488859"] |
+-----------+----------------------------+---------+---+----------+-----------------------------+
| ["person" | "person:36152353956560906" | "likes" | 0 | "post" | "post:108209947994488860"] |
+-----------+----------------------------+---------+---+----------+-----------------------------+
| ["post" | "post:108209947994488860" | "likes" | 0 | "person" | "person:36152353956560906"] |
+-----------+----------------------------+---------+---+----------+-----------------------------+
| ["post" | "post:108209947994488859" | "likes" | 0 | "person" | "person:36152353956560906"] |
+-----------+----------------------------+---------+---+----------+-----------------------------+
随机游走(random_walk)
概述
随机游走算法是一种基于概率的图遍历算法,它模拟在图或网络中的随机移动过程。该算法从一个起始点开始,按照一定的概率选择下一个点,并重复该过程,直到满足停止条件。随机游走算法可以用于推荐系统中,通过在用户-物品关系图上进行随机游走,发现潜在的兴趣和关联关系,从而进行个性化的推荐。随机游走算法还可以作为图嵌入和图学习的基础,通过捕捉点之间的随机游走路径,将图结构转化为向量表示,用于机器学习任务,如点分类、链接预测等。
语法
MATCH ... call random_walk($(path), $(nodes), $(length))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| nodes | List | 否 | 起点列表 | '[36152353956560896, 36152353956560897]' | ||
| length | int | 否 | 随机游走长度 | 5 |
结果输出
| 名称 | 描述 |
|---|---|
| 0 | 游走路径 |
示例
查询语句
MATCH (n:person)-[e:likes]->(b:post) call random_walk((n)-[e]->(b), '[36152353956560896, 36152353956560897]', 3)
YIELD task_id
RETURN task_id;
直径估计算法(diameter)
概述
直径估计算法是一种用于估计图的直径(即最长的最短路径长度)的算法。图的直径是指图中任意两个点之间最短路径的最大长度,它是描述图大小和连接性的重要指标之一。
直径估计算法的目标是在不计算所有点对之间的精确最短路径的情况下,给出一个对直径的近似估计值。这是因为在大规模的图中,计算所有点对之间的最短路径是非常耗时和资源密集的操作。因此,直径估计算法通过使用采样、近似或其他快速计算方法,提供一个接近实际直径值的估计结果。
直径估计算法通过提供对图直径的近似估计,为大规模图的分析和应用提供了高效的解决方案。它在许多领域中都有重要的应用,帮助人们理解和利用复杂的图结构。
语法
MATCH ... call diameter($(path), $(sample), $(weight))
YIELD *
RETURN *;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| sample | int | 否 | 抽样数 | 10 | ||
| weight | Property | 否 | 权重属性, | e.weight |
结果输出
| 名称 | 描述 |
|---|---|
| 0 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call diameter((n)-[e]->(b),10, e.weight)
YIELD task_id
RETURN task_id; - 期望结果
+-----+
| 0 |
+=====+
| 0.6 |
+-----+
点边界(node_boundary)
概述
顶点边界为图内两个子图T和S的边界点集合,集合内每个点都在T中,且存在一条边连接到S中的点。
在社交网络和关系网络中,Node Boundary 的应用很广泛,例如在社交网络中,Node Boundary 可以用于识别社区的边界节点和“桥接节点”�,这些节点可以促进不同社区之间的联系和信息传递。
语法
MATCH ... call node_boundary($(path), $(nbunch1), $(nbunch2))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| nbunch1 | List | 否 | 点列表1 | '[36152353956560896, 36152353956560897]' | ||
| nbunch2 | List | 否 | 点列表2 | '[108209947994488858, 108209947994488859]' |
结果输出
| 名称 | 描述 |
|---|---|
| 0 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call node_boundary((n)-[e]->(b), '[36152353956560896,36152353956560897]','[108209947994488858,108209947994488859]')
YIELD task_id
RETURN task_id;
SHOW JOB xxx RESULTS limit 10; - 期望结果
+--------------------+
| 0 |
+====================+
| 108209947994488859 |
+--------------------+
边边界(edge_boundary)
概述
edge Boundary(边界边)是指连接着两个不同社区的边。边界边算法则是指一种用于识别边界边的算法,其主要目的是确定社区之间的边界,并促进不同社区之间的联系和信息传递。边界边算法通常是基于图的拓扑结构和社区特征的分析,在社交网络、关系网络、Web网页链接分析等领域都有广泛的应用。
语法
MATCH ... call edge_boundary($(path), $(nbunch1), $(nbunch2))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| nbunch1 | List | 否 | 点列表1 | '[36152353956560896, 36152353956560897]' | ||
| nbunch2 | List | 否 | 点列表2 | '[108209947994488858, 108209947994488859]' |
结果输出
| 名称 | 描述 |
|---|---|
| 0 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call edge_boundary((n)-[e]->(b), '[36152353956560896, 36152353956560897]','[108209947994488858, 108209947994488859]')
YIELD task_id
RETURN task_id; - 期望结果
+-------------------+--------------------+
| 0 | 1 |
+===================+====================+
| 36152353956560897 | 108209947994488859 |
+-------------------+--------------------+
| 36152353956560896 | 108209947994488859 |
+-------------------+--------------------+
节点对最短路径(all_shortest_path)
概述
查询一个起点和一个终点之间的所有最短路径。
语法
MATCH ... CALL all_shortest_path((n)-[e]->(b), $(source), $(target), $(k), $(directed),$(weight), $(weight property))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| sourcce | int | 否 | 起始点, 格式为 点类型:点id | 36152353956560896 | ||
| target | int | 否 | 起始点, 格式为 点类型:点id | 36152353956560896 | ||
| k | int | 否 | 最大跳数 | 3 | ||
| directed | int | 否 | 边方向 0:out, 1:in , 2:both | 2 | ||
| weight | str | 否 | 权重属性名字 | "weight" | ||
| property | Property | 否 | 权重属性 | e.weight |
结果输出
| 名称 | 描述 |
|---|---|
| 0 | 最短路径 |
示例
-
查询语句
MATCH (n:person)-[e:knows]->(b:person) call all_shortest_path((n)-[e]->(b), 36152353956560896, 36152353956560898, 5, 2,"weight", e.weight)
YIELD task_id
RETURN task_id; -
期望结果
+--------------------+----------+-------------------+-----------+
| 0 | | | |
+====================+==========+===================+===========+
| [36152353956560900 | "person" | 36152353956560898 | "person"] |
+--------------------+----------+-------------------+-----------+
| [36152353956560897 | "person" | 36152353956560900 | "person"] |
+--------------------+----------+-------------------+-----------+
| [36152353956560896 | "person" | 36152353956560897 | "person"] |
+--------------------+----------+-------------------+-----------+
所有简单路径(all_simple_paths)
概述
查询一个起点经过给定点的所有简单路径。
语法
MATCH ... CALL all_simple_paths((n)-[e]->(b), $(nodes), $(src), $(k))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| nodes | list | 否 | 点列表 | '[108209947994488859]' | ||
| src | str | 否 | 起始点, 格式为 点类型:点id | 36152353956560896 | ||
| k | int | 否 | 最大跳数 | 3 |
结果输出
| 名称 | 描述 |
|---|---|
| 0 | 简单路径 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call all_simple_paths((n)-[e]->(b), '[108209947994488859]', 36152353956560896, 10)
YIELD task_id
RETURN task_id; - 期望结果
+--------------------+---------------------+
| 0 | |
+====================+=====================+
| [36152353956560896 | 108209947994488859] |
+--------------------+---------------------+
所有点对最短路径长度(sssp_all_pairs_length)
概述
所有点之间的最短路径长度。
语法
MATCH ... CALL sssp_all_pairs_length($(path), $(weight))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| weight | Property | 否 | 权重属性 | e.weight |
结果输出
| 名称 | 描述 |
|---|---|
| result | 平均最短路径长度 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call sssp_all_pairs_length((n)-[e]->(b), e.weight)
YIELD task_id
RETURN task_id; - 期望结果
+--------------------+--------------------+------+
| 0 | | |
+====================+====================+======+
| [0 | 36152353956560897 | 0.0] |
+--------------------+--------------------+------+
| [1 | 36152353956560896 | 0.0] |
+--------------------+--------------------+------+
| [2 | 36152353956560898 | 0.0] |
+--------------------+--------------------+------+
| [3 | 36152353956560906 | 0.0] |
+--------------------+--------------------+------+
| [4 | 36152353956560907 | 0.0] |
+--------------------+--------------------+------+
| [0 | 108209947994488859 | 0.3] |
+--------------------+--------------------+------+
| [1 | 108209947994488859 | 0.1] |
+--------------------+--------------------+------+
| [3 | 108209947994488859 | 0.1] |
+--------------------+--------------------+------+
| [4 | 108209947994488859 | 0.1] |
+--------------------+--------------------+------+
| [72057594037927936 | 108209947994488859 | 0.0] |
+--------------------+--------------------+------+
| [1 | 108209947994488860 | 0.6] |
+--------------------+--------------------+------+
| [3 | 108209947994488860 | 0.6] |
+--------------------+--------------------+------+
| [4 | 108209947994488860 | 0.6] |
+--------------------+--------------------+------+
| [72057594037927937 | 108209947994488860 | 0.0] |
+--------------------+--------------------+------+
| [2 | 108209947994488858 | 0.3] |
+--------------------+--------------------+------+
| [72057594037927938 | 108209947994488858 | 0.0] |
+--------------------+--------------------+------+
深度优先搜索(dfs)
概述
通过深度优先搜索查找各个点到起点的距离。
语法
MATCH ... call dfs($(path), $(src))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| src | int | 否 | 起始点, 格式为 点oid | 36152353956560896 |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点 ID |
| result | 与起始点的距离 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call dfs((n)-[e]->(b), 36152353956560896)
YIELD task_id
RETURN task_id; - 期望结果
+--------------------+--------+
| id | result |
+====================+========+
| 36152353956560897 | -1 |
+--------------------+--------+
| 36152353956560896 | 0 |
+--------------------+--------+
| 36152353956560898 | -1 |
+--------------------+--------+
| 36152353956560906 | -1 |
+--------------------+--------+
| 36152353956560907 | -1 |
+--------------------+--------+
| 108209947994488859 | 1 |
+--------------------+--------+
| 108209947994488860 | 2 |
+--------------------+--------+
| 108209947994488858 | -1 |
+--------------------+--------+
多源多跳(multi_source_khop)
概述
查找多个源头定点的K跳的结果(支持返回K跳的点或者k跳的点的数量)。
语法
MATCH ... CALL multi_source_khop($(path), $(src_ids), $(v_type),$(e_type),$(dir),$(khop1),$(khop2),$(count))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| src_ids | int | 否 | 起始点, 格式为 '["点类型:点id",...]' | '[36152353956560896,36152353956560897]' | ||
| v_type | str | 否 | 点类型名称 | "person" | ||
| e_type | str | 否 | 边类型名称 | "knows" | ||
| dir | int | 否 | 方向, 0:out 1:in 2:both | 2 | ||
| khop1 | int | 否 | 跳数下限(含) | 1 | ||
| khop2 | int | 否 | 跳数上限(含) | 3 | ||
| count | bool | FALSE | 是 | 是否统计数量,而不返回具体的目标点Id | FALSE |
结果输出
| 名称 | 描述 |
|---|---|
| id | 起点 ID |
| result | 目标点 ID 或者目标点数量 |
示例
- 查询语句
//返回顶点
MATCH (n:person)-[e:knows]->(b:person) call multi_source_khop((n)-[e]->(b), '[36152353956560896,36152353956560897]', "person","knows",2,1,3,false)
YIELD task_id
RETURN task_id;
//返回数量
MATCH (n:person)-[e:knows]->(b:person) call multi_source_khop((n)-[e]->(b), '[36152353956560896,36152353956560897]', "person","knows",2,1,3,true)
YIELD task_id
RETURN task_id; - 期望结果
//返回顶点
+--------------------+-----------------------------+
| 0 | |
+====================+=============================+
| [36152353956560896 | "person:36152353956560897"] |
+--------------------+-----------------------------+
| [36152353956560896 | "person:36152353956560903"] |
+--------------------+-----------------------------+
| [36152353956560896 | "person:36152353956560910"] |
+--------------------+-----------------------------+
| [36152353956560896 | "person:36152353956560902"] |
+--------------------+-----------------------------+
| [36152353956560896 | "person:36152353956560901"] |
+--------------------+-----------------------------+
| [36152353956560896 | "person:36152353956560900"] |
+--------------------+-----------------------------+
| [36152353956560896 | "person:36152353956560898"] |
+--------------------+-----------------------------+
| [36152353956560897 | "person:36152353956560903"] |
+--------------------+-----------------------------+
| [36152353956560897 | "person:36152353956560904"] |
+--------------------+-----------------------------+
| [36152353956560897 | "person:36152353956560910"] |
+--------------------+-----------------------------+
| [36152353956560897 | "person:36152353956560905"] |
+--------------------+-----------------------------+
| [36152353956560897 | "person:36152353956560902"] |
+--------------------+-----------------------------+
| [36152353956560897 | "person:36152353956560901"] |
+--------------------+-----------------------------+
| [36152353956560897 | "person:36152353956560896"] |
+--------------------+-----------------------------+
| [36152353956560897 | "person:36152353956560899"] |
+--------------------+-----------------------------+
| [36152353956560897 | "person:36152353956560900"] |
+--------------------+-----------------------------+
| [36152353956560897 | "person:36152353956560898"] |
+--------------------+-----------------------------+
//返回数量
+--------------------+-----+
| 0 | |
+====================+=====+
| [36152353956560896 | 7] |
+--------------------+-----+
| [36152353956560897 | 10] |
+--------------------+-----+
通用广度优先搜索(bfs)
概述
通用广度优先搜索。
HTAP语法
MATCH ... call bfs_generic($(path), $(src), $(limit), $(format))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|
| src | int | 0 | 否 | 起始点oid | 36152353956560896 |
| limit | int | 10 | 否 | 返回个数 | 10 |
| format | str | predecessors | 否 | 输出格式,edges/predecessors/successors | predecessors |
- HTAP参数
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) |
结果输出
- format=predecessors
| 名称 | 描述 |
|---|---|
| id | 点 ID |
| result |
示例
-
HTAP查询语句
MATCH (n:person)-[e:likes]->(b:post) call bfs_generic((n)-[e]->(b), 36152353956560896, 10, "predecessors")
YIELD task_id
RETURN task_id; -
HTTP请求
curl -X 'POST' 'http://localhost:8000/graph-computing/' -H 'accept: application/json' -H 'Content-Type: application/json' -d '{"algorithmName": "bfs", "graphName": "LDBC_SNB", "taskId": "bfs", "subGraph": {"edgeTypes": [{"edgeTypeName": "knows", "vertexPairs": [{"fromName": "person", "toName": "person"}]}], "vertexTypes": [{"vertexTypeName": "person"}]}, "algorithmParams": {"src": 0}}' -
期望结果
+--------------------+-------------------+
| 0 | 1 |
+====================+===================+
| 108209947994488859 | 36152353956560896 |
+--------------------+-------------------+
| 108209947994488860 | 36152353956560896 |
+--------------------+-------------------+
度中心性(degree_centrality)
概述
计算图中每一个点的归一化度数。其中归一化度数为度数除以最大可能度数,对于一个包含 n 个点的简单图来说,任一点的最大可能度数为 n-1。一个点的度(数)越大,意味着该点的度中心性越高,就说明在图中这个点越重要。
主要应用于社会网络分析、网络用户行为分析、信用网络分析、图论研究、负复杂网络研究、脑功能网络分析、欺诈网络分析等场景。例如,在一个社交网络中,一个拥有更多度(数)的人(点)更容易与其他人(点)发生直接接触,也更容易获得流感。
语法
MATCH ... call degree_centrality($(path), $(centrality_type))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| centrality_type | str | 否 | 边方向, in 或 out 或 both | "both" |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点 ID |
| result | 点对应的中心度值 |
示例
-
查询语句
MATCH (n:person)-[e:likes]->(b:post) call degree_centrality((n)-[e]->(b), "both")
YIELD task_id
RETURN task_id; -
期望结果
+--------------------+--------------------+
| id | result |
+====================+====================+
| 36152353956560897 | 0.1428571428571428 |
+--------------------+--------------------+
| 36152353956560896 | 0.2857142857142857 |
+--------------------+--------------------+
| 36152353956560898 | 0.1428571428571428 |
+--------------------+--------------------+
| 36152353956560906 | 0.2857142857142857 |
+--------------------+--------------------+
| 36152353956560907 | 0.2857142857142857 |
+--------------------+--------------------+
| 108209947994488859 | 0.5714285714285714 |
+--------------------+--------------------+
| 108209947994488860 | 0.4285714285714285 |
+--------------------+--------------------+
| 108209947994488858 | 0.1428571428571428 |
+--------------------+--------------------+
特征向量中心度(eigenvector_centrality)
概述
计算图的特征向量中心性。根据给定点的邻居点的数量(给定点的度数)计算给定点的中心性。特征向量中心度算法用来度量点之间的传递影响和连通性,考虑点传递影响的中心度测量方法,而不是考虑点的直接重要性。在特征向量中心度算法中,其认为与具有高得分的点相连接比与具有低得分的点相连接所得的贡献更大。
语法
MATCH ... call eigenvector_centrality($(path), $(tolerance), $(max_round))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| tolerance | Double | 否 | 收敛偏差,即归一化后的向量所有元素绝对值的和的变化,若变化值小于收敛偏差,则算法结束 | 0.3 | ||
| max_round | int | 否 | 最大迭代轮数 | 10 |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点 ID |
| result | 点对应的中心度值 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call eigenvector_centrality((n)-[e]->(b), 0.3, 3)
YIELD task_id
RETURN task_id; - 期望结果
+--------------------+--------------------+
| id | result |
+====================+====================+
| 36152353956560897 | 0.1414213562373095 |
+--------------------+--------------------+
| 36152353956560896 | 0.1414213562373095 |
+--------------------+--------------------+
| 36152353956560898 | 0.1414213562373095 |
+--------------------+--------------------+
| 36152353956560906 | 0.1414213562373095 |
+--------------------+--------------------+
| 36152353956560907 | 0.1414213562373095 |
+--------------------+--------------------+
| 108209947994488859 | 0.7071067811865475 |
+--------------------+--------------------+
| 108209947994488860 | 0.565685424949238 |
+--------------------+--------------------+
| 108209947994488858 | 0.282842712474619 |
+--------------------+--------------------+
Katz中心性(katz_centrality)
概述
计算图 G 点的 Katz 中心性。基于其邻居的中心性来计算点的中心性,是特征向量中心性算法的推广。Katz 中心性算法通过测量相邻点和网络中通过这些相邻点连接到点的所有其他点的数量,计算网络中点的相对影响。
语法
MATCH ... call katz_centrality($(path), $(alpha), $(beta), $(tolerance), $(max_round), $(normalized))
YIELD *
RETURN *;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| alpha | double | 否 | 衰减因子 | 0.1 | ||
| beta | double | 否 | 分配给直接邻点的权重 | 1.0 | ||
| tolerance | double | 否 | 误差容忍 | 0.000006 | ||
| max_round | int | 否 | 最大轮数 | 10 | ||
| normalized | bool | 否 | 是否归一化 | TRUE | ||
| degree_threshold | int | 否 | 过滤度大于阈值的超级点 | 1000000 |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点 ID |
| result |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call katz_centrality((n)-[e]->(b), 0.1, 1.0, 0.1, 3, true, 2)
YIELD task_id
RETURN task_id; - 期望结果
+--------------------+--------------------+
| id | result |
+====================+====================+
| 36152353956560897 | 0.4012861768466446 |
+--------------------+--------------------+
| 36152353956560896 | 0.4012861768466446 |
+--------------------+--------------------+
| 36152353956560898 | 0.4012861768466446 |
+--------------------+--------------------+
| 36152353956560906 | 0.4012861768466446 |
+--------------------+--------------------+
| 36152353956560907 | 0.4012861768466446 |
+--------------------+--------------------+
| 108209947994488859 | 0.0 |
+--------------------+--------------------+
| 108209947994488860 | 0.0 |
+--------------------+--------------------+
| 108209947994488858 | 0.4414147951292721 |
+--------------------+--------------------+
投票排名算法(voterank)
概述
基于投票方案计算图中的点的排名。每轮迭代,所有剩余点都投票�给它的每个近邻,投票最高的点被迭代地选举出来,对点的重要性进行排序。
语法
MATCH ... CALL voterank($(path), $(seeds))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| seeds | List | 否 | seeds 点列表 | '[36152353956560907]' |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点 ID |
| result | 中心度,重要性 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call voterank((n)-[e]->(b), '[36152353956560907]')
YIELD task_id
RETURN task_id; - 期望结果
+--------------------+--------------------+
| id | result |
+====================+====================+
| 36152353956560897 | 0.0589794027414828 |
+--------------------+--------------------+
| 36152353956560896 | 0.0589794027414828 |
+--------------------+--------------------+
| 36152353956560898 | 0.0589794027414828 |
+--------------------+--------------------+
| 36152353956560906 | 0.0589794027414828 |
+--------------------+--------------------+
| 36152353956560907 | 0.2089794027414828 |
+--------------------+--------------------+
| 108209947994488859 | 0.2480617917755513 |
+--------------------+--------------------+
| 108209947994488860 | 0.1979288361619239 |
+--------------------+--------------------+
| 108209947994488858 | 0.1091123583551102 |
+--------------------+--------------------+
紧密中心度(closeness_centrality)
概述
Closeness centrality(紧密中心度)是一种社会网络分析中常用的中心性度量方式,用于衡量点与其他点之间的接近程度。它是通过计算点到其他点的平均最短路径长度来判断点的重要性。接近中心性越高的点,其到其他点的平均最短路径长度越短,因此在信息传播、影响力传播和资源流动等方面具有较强的影响力。
语法
MATCH ... call closeness_centrality($(path), $(wf_improved))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| wf_improved | bool | 否 | 是否启用 Wasserman and Faust | FALSE |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点 ID |
| result | 中心度值 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call closeness_centrality((n)-[e]->(b), false)
YIELD task_id
RETURN task_id; - 期望结果
+--------------------+--------------------+
| id | result |
+====================+====================+
| 36152353956560897 | 0.0 |
+--------------------+--------------------+
| 36152353956560896 | 0.0 |
+--------------------+--------------------+
| 36152353956560898 | 0.0 |
+--------------------+--------------------+
| 36152353956560906 | 0.0 |
+--------------------+--------------------+
| 36152353956560907 | 0.0 |
+--------------------+--------------------+
| 108209947994488859 | 0.5714285714285714 |
+--------------------+--------------------+
| 108209947994488860 | 0.4285714285714285 |
+--------------------+--------------------+
| 108209947994488858 | 0.1428571428571428 |
+--------------------+--------------------+
介数中心度(betweenness_centrality)
概述
介数中心度(Betweenness Centrality)是一种用于衡量网络中点重要性的指标。它反映了点在网络中作为中介者的程度,即点在网络中连接其他点的重要性。介数中心度的值越高,表示该点在网络中的中介地位越重要。介数中心度算法的基本思想是通过计算所有点对之间的最短路径数量,来估算每个点的介数中心度。
在社交网络中,介数中心度可以用来识别关键的中间人,即那些在信息传播和社交互动中发挥重要作用的人物。这对于寻找潜在的影响者、社群发现和信息传播的研究非常有用。在交通网络中,介数中心度可以用来识别那些在交通流量中扮演关键角色的点。这对于优化交通路线、改善交通流动性以及设计公共交通系统非常重要。
语法
MATCH ... call betweenness_centrality($(path), $(normalized), $(endpoints))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| normalized | Boolean | 否 | 结果是否归一化 | TRUE | ||
| endpoints | Boolean | 否 | 是否将该点计入到最短路径计数 | TRUE |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点 ID |
| result | 点对应的 pagerank 值 |
示例
-
查询语句
MATCH (n:person)-[e:likes]->(b:post) call betweenness_centrality((n)-[e]->(b), false, false)
YIELD task_id
RETURN task_id; -
期望结果
+--------------------+--------+
| id | result |
+====================+========+
| 36152353956560897 | 0.0 |
+--------------------+--------+
| 36152353956560896 | 0.0 |
+--------------------+--------+
| 36152353956560898 | 0.0 |
+--------------------+--------+
| 36152353956560906 | 0.0 |
+--------------------+--------+
| 36152353956560907 | 0.0 |
+--------------------+--------+
| 108209947994488859 | 0.0 |
+--------------------+--------+
| 108209947994488860 | 0.0 |
+--------------------+--------+
| 108209947994488858 | 0.0 |
+--------------------+--------+
边介数中心度(edge_betweenness_centrality)
概述
边介数中心度(Edge Betweenness Centrality)是一种用于衡量网络中边(或连接)重要性的指标。与节点介数中心度类似,边介数中心度也关注网络中的中介地位,但它衡量的是边在网络中作为桥梁的程度,即边在连接点之间的重要性。边介数中心度的值越高,表示该边在网络中作为连接路径的重要性越大。通过计算边介数中心度,我们可以识别那些在网络中承担关键连接作用的边。
通过计算边介数中心度,可以识别网络中连接不同社区的桥梁边。这些桥梁边在网络社区发现中具有重要的作用,帮助发现社区之间的连接和潜在的过渡点。在电力网络和交通网络中,边介数中心度可以用来识别关键的连接线路或路径。通过识别具有高边介数中心度的边,可以找到那些在能源传输或交通流动中起关键作用的线路或路径,从而优化网络的可靠性和效率。在社交媒体或信息传播网络中,边介数中心度可以用于研究信息传播的路径和关键影响者。识别具有高边介数中心度的边,可以帮助我们理解信息传播的路径和扩散的影响力。
语法
MATCH ... call edge_betweenness_centrality($(path), $(normalized))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| normalized | Boolean | 否 | 结果是否归一化 | TRUE |
结果输出
| 名称 | 描述 |
|---|---|
| 0 | 每个边及边介数中心度 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call edge_betweenness_centrality((n)-[e]->(b), false)
YIELD task_id
RETURN task_id; - 期望结果
+--------------------+--------------------+-----------------------+
| 0 | | |
+====================+====================+=======================+
| [36152353956560897 | 108209947994488859 | 0.023809523809523809] |
+--------------------+--------------------+-----------------------+
| [36152353956560896 | 108209947994488859 | 0.023809523809523809] |
+--------------------+--------------------+-----------------------+
| [36152353956560896 | 108209947994488860 | 0.023809523809523809] |
+--------------------+--------------------+-----------------------+
| [36152353956560898 | 108209947994488858 | 0.023809523809523809] |
+--------------------+--------------------+-----------------------+
| [36152353956560906 | 108209947994488859 | 0.023809523809523809] |
+--------------------+--------------------+-----------------------+
| [36152353956560906 | 108209947994488860 | 0.023809523809523809] |
+--------------------+--------------------+-----------------------+
| [36152353956560907 | 108209947994488859 | 0.023809523809523809] |
+--------------------+--------------------+-----------------------+
| [36152353956560907 | 108209947994488860 | 0.023809523809523809] |
+--------------------+--------------------+-----------------------+
网页排名(pagerank)
概述
给每个节点附加权值,对节点的重要性进行排序。 输入是一个有向图G,顶点表示网页。如果存在网页A到网页B的连接,则存在连接A到B的边。不同的网页之间相互引用,网页作为节点,引用关系作为边,被更多网页引用的网页具有更高的权重。 如果一个网页被很多其他网页连接到,说明这个网页比较重要,也就是其PageRank值会相对较高。如果一个PageRank值很高的网页连接到其他网页,那么被连接到的网页的 PageRank值会相应地提高。 适用于网页排序、社交网络重点人物发掘等场景。比如,一个新开的网站N只有两个页面指向它的超链接,一个来自著名且历史悠久的门户网站F,另一个来自鲜有人知的网站U,那么根据PageRank计算,会得到新网站N比F网站更优质的结论。
语法
MATCH ... call pagerank($(path), $(delta), $(maxround), $(weight))
YIELD *
RETURN *;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| delta | double | 否 | 阻尼系数 | 0.85 | ||
| maxRound | int | 否 | 迭代轮数 | 100 | ||
| weight | Property | 是 | 权重字段 | e.weight |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点 ID |
| result | 点对应的pagerank值 |
示例
-
查询语句
//不带权重字段
MATCH (n:person)-[e:knows]->(b:person) call pagerank((n)-[e]->(b), 0.85, 10) YIELD * RETURN task_id;
//带权重字段
MATCH (n:person)-[e:knows]->(b:person) call pagerank((n)-[e]->(b), 0.85, 10, e.weight) YIELD * RETURN task_id; -
期望结果
//不带权重
+-------------------+--------------------+
| id | result |
+===================+====================+
| 36152353956560897 | 0.0343178949156211 |
+-------------------+--------------------+
| 36152353956560903 | 0.1655306491067044 |
+-------------------+--------------------+
| 36152353956560904 | 0.0968003536898267 |
+-------------------+--------------------+
| 36152353956560910 | 0.0343178949156211 |
+-------------------+--------------------+
| 36152353956560908 | 0.0381054010765945 |
+-------------------+--------------------+
| 36152353956560905 | 0.1790136826750931 |
+-------------------+--------------------+
| 36152353956560902 | 0.0364494358013219 |
+-------------------+--------------------+
| 36152353956560901 | 0.0453980445770397 |
+-------------------+--------------------+
| 36152353956560896 | 0.0267428825936744 |
+-------------------+--------------------+
| 36152353956560899 | 0.0267428825936744 |
+-------------------+--------------------+
| 36152353956560900 | 0.0551045977846872 |
+-------------------+--------------------+
| 36152353956560898 | 0.0440244481232686 |
+-------------------+--------------------+
| 36152353956560906 | 0.0267428825936744 |
+-------------------+--------------------+
| 36152353956560907 | 0.1907089495531981 |
+-------------------+--------------------+
//带权重
+-------------------+--------------------+
| id | result |
+===================+====================+
| 36152353956560897 | 0.0343178949156211 |
+-------------------+--------------------+
| 36152353956560903 | 0.1655306491067044 |
+-------------------+--------------------+
| 36152353956560904 | 0.0968003536898267 |
+-------------------+--------------------+
| 36152353956560910 | 0.0343178949156211 |
+-------------------+--------------------+
| 36152353956560908 | 0.0381054010765945 |
+-------------------+--------------------+
| 36152353956560905 | 0.1790136826750931 |
+-------------------+--------------------+
| 36152353956560902 | 0.0364494358013219 |
+-------------------+--------------------+
| 36152353956560901 | 0.0453980445770397 |
+-------------------+--------------------+
| 36152353956560896 | 0.0267428825936744 |
+-------------------+--------------------+
| 36152353956560899 | 0.0267428825936744 |
+-------------------+--------------------+
| 36152353956560900 | 0.0551045977846872 |
+-------------------+--------------------+
| 36152353956560898 | 0.0440244481232686 |
+-------------------+--------------------+
| 36152353956560906 | 0.0267428825936744 |
+-------------------+--------------------+
| 36152353956560907 | 0.1907089495531981 |
+-------------------+--------------------+
sybil指数(sybil_rank)
概述
与信任指数算法类似,Sybil 指数算法也用于垃圾点检测,不同的是 sybilrank 是通过提前终止的随机游走对网络中点的可信度进行排名的算法,主要应用于在线社交网络(Online Social Network, OSN)。OSN 的普及伴随着越来越多的 Sybil 攻击,恶意攻击者会创建多个虚假账户(Sybils),目的是发送垃圾邮件、分发恶意软件、操纵投票或内容浏览量等。
语法
MATCH ... call sybil_rank($(path), $(total_trust), $(sources), $(max_iter))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| total_trust | double | 否 | 总分 | 100 | ||
| sources | List | 否 | 初始点列表 | '[36152353956560896, 36152353956560897]' | ||
| max_iter | Property Expression | 否 | 最大迭代次数 | 100 |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点 ID |
| result | 中心度 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call sybil_rank((n)-[e]->(b), 100.0,'[36152353956560896, 36152353956560897]', 100)
YIELD task_id
RETURN task_id; - 期望结果
+--------------------+-------------------+
| id | result |
+====================+===================+
| 36152353956560897 | 0.0 |
+--------------------+-------------------+
| 36152353956560896 | 0.0 |
+--------------------+-------------------+
| 36152353956560898 | 0.0 |
+--------------------+-------------------+
| 36152353956560906 | 0.0 |
+--------------------+-------------------+
| 36152353956560907 | 0.0 |
+--------------------+-------------------+
| 108209947994488859 | 57.14285714285715 |
+--------------------+-------------------+
| 108209947994488860 | 42.85714285714286 |
+--------------------+-------------------+
| 108209947994488858 | 0.0 |
+--------------------+-------------------+
链接分析(HITS)
概述
HITS 算法是一种基于链接分析的点(网页)评级算法,其主要目的是通过一定的手段在海量网页中找到与用户查询主题相关的优质 Hub 页面和 Authority 页面。因为这些页面代表了能够满足用户查询的高质量内容。在 HITS 算法中,每个页面的链接质量由 Hub 值和 Authority 值共同决定。具体地:
- Hub 值:每个页面的 Hub 值等于其指向的所有页面的 Authority 值之和。换句话说,一个页面的 Hub 值反映了这个页面所链接的其他页面的质量。
- Authority 值:每个页面的 Authority 值等于其被所有指入的页面的 Hub 值之和。这个值反映了一个页面被其他页面的链接的质量。
因此,HITS 算法中的 Hub 值和 Authority 值之间存在一种相互权衡的关系:一个页面指向的链接权威值越高,其 Hub 值越大;而 Hub 值越大,则说明指向该页面的权威值越高。
以下是两个应用 HITS 算法的场景:
-
应用场景 1:利用 HITS 枢纽页面与权威页面之间的关系提升排名卡位现象。�例如,对于排名第三页的情况,可以通过 HITS 算法优化枢纽页面和权威页面的关系,实现少许排名提升的目标。
-
应用场景 2:利用 HITS 带动其他页面之间的排名。例如,在优化某个页面的同时,可以利用 HITS 算法中的优质 Hub 页面和 Authority 页面的关系,带动没有优化过的页面的排名提升。
语法
MATCH ... call hits($(path), $(tolerance), $(max_round), $(normalized))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| tolerance | double | 否 | 误差容忍 | 0.000006 | ||
| max_round | int | 否 | 最大轮数 | 10 | ||
| normalized | bool | 否 | 是否归一化 | TRUE |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点 ID |
| hub | hub 值 |
| auth | authority 值 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call hits((n)-[e]->(b), 0.1, 3, true)
YIELD task_id
RETURN task_id; - 期望结果
+--------------------+--------------------+--------------------+
| id | hub | auth |
+====================+====================+====================+
| 36152353956560897 | 0.1527647610121837 | 0.0 |
+--------------------+--------------------+--------------------+
| 36152353956560896 | 0.282099343955014 | 0.0 |
+--------------------+--------------------+--------------------+
| 36152353956560898 | 0.0009372071227741 | 0.0 |
+--------------------+--------------------+--------------------+
| 36152353956560906 | 0.282099343955014 | 0.0 |
+--------------------+--------------------+--------------------+
| 36152353956560907 | 0.282099343955014 | 0.0 |
+--------------------+--------------------+--------------------+
| 108209947994488859 | 0.0 | 0.5397350993377483 |
+--------------------+--------------------+--------------------+
| 108209947994488860 | 0.0 | 0.4569536423841059 |
+--------------------+--------------------+--------------------+
| 108209947994488858 | 0.0 | 0.0033112582781456 |
+--------------------+--------------------+--------------------+
三角计数(triangles)
概述
计算图中每个点的三角形数量。用于社区发现,衡量社区耦合关系的紧密程度。比如一个图中有很多三角形,说明该社区很稳定,点间联系比较紧密。适用于衡量图的结构特性场景。
语法
MATCH ... call triangles($(path))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) |
结果输出
| 名称 | 描述 |
|---|---|
| 0 | 每个顶点及三角形数量 |
示例
- 查询语句
MATCH (n:person)-[e:knows]->(b:person) call triangles((n)-[e]->(b))
YIELD task_id
RETURN task_id;
聚类系数(clustering)
概述
计算图中每个节点的聚类系数。聚类系数反映了与该节点相关联的节点彼此有关联的概率。适用于衡量图的结构特性场景。
语法
MATCH ... CALL clustering($(path), $(degree_threshold))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| degree_threshold | int | 否 | 度阈值 | 10 |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点 ID |
| result | 中心度 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call clustering((n)-[e]->(b), 3)
YIELD task_id
RETURN task_id; - 期望结果
+--------------------+--------+
| id | result |
+====================+========+
| 36152353956560897 | 0.0 |
+--------------------+--------+
| 36152353956560896 | 0.0 |
+--------------------+--------+
| 36152353956560898 | 0.0 |
+--------------------+--------+
| 36152353956560906 | 0.0 |
+--------------------+--------+
| 36152353956560907 | 0.0 |
+--------------------+--------+
| 108209947994488859 | 0.0 |
+--------------------+--------+
| 108209947994488860 | 0.0 |
+--------------------+--------+
| 108209947994488858 | 0.0 |
+--------------------+--------+
平均聚类系数(avg_clustering)
概述
计算图中所有点聚类系数的平均值。
语法
MATCH ... CALL avg_clustering($(path), $(degree_threshold))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| degree_threshold | int | 否 | 度阈值 | 10' |
结果输出
| 名称 | 描述 |
|---|---|
| 0 | 图平均聚类系数,平均聚类系数的取值范围为 0~1。 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call avg_clustering((n)-[e]->(b), 10)
YIELD task_id
RETURN task_id; - 期望结果
+-----+
| 0 |
+=====+
| 0.0 |
+-----+
传递性(transitivity)
概述
传递性用来衡量相邻顶点共享相同的邻居顶点的比例,计算方法为图中三角形数量和可能三角形(顶点及其任意两个邻居顶点都有可能构成三角形)的比值。
语法
MATCH ... call transitivity($(path))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) |
结果输出
| 名称 | 描述 |
|---|---|
| 0 | 图中实际存在的三角形数量与所有可能由顶点及其邻居顶点构成的三角形数量的比值。 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call transitivity((n)-[e]->(b))
YIELD task_id
RETURN task_id; - 期望结果
+-----+
| 0 |
+=====+
| 0.0 |
+-----+
弱连通分量(wcc)
概述
给定无向图,弱连通分量(WCC)是原始图的一个子图,其中所有的顶点都通过某种路径相互连接,忽略了边的方向。
语法
MATCH ... call wcc($(path))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点 ID |
| result | 联通分量号 |
示例
- 查询语句
MATCH (n:person)-[e:knows]->(b:person) call wcc((n)-[e]->(b))
YIELD task_id
RETURN task_id;
弱连通分量数(number_connected_components)
概述
给定无�向图,返回弱连通分量子图个数。
语法
MATCH ... call number_connected_components($(path))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) |
结果输出
| 名称 | 描述 |
|---|---|
| 0 | 联通分量数 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call number_connected_components((n)-[e]->(b))
YIELD task_id
RETURN task_id; - 期望结果
+---+
| 0 |
+===+
| 2 |
+---+
强连通分量(scc)
概述
给定有向图,强连通分量(SCC)是原始图的一个子图,其中所有的顶点都通过某种路径相互可达。
语法
MATCH ... call scc($(path))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点ID |
| result | 连通分量id |
示例
- 查询语句
MATCH (n:person)-[e:knows]->(b:person) call scc((n)-[e]->(b))
YIELD task_id
RETURN task_id; - 期望结果
+-------------------+--------+
| id | result |
+===================+========+
| 36152353956560897 | 0 |
+-------------------+--------+
| 36152353956560903 | 1 |
+-------------------+--------+
| 36152353956560904 | 2 |
+-------------------+--------+
| 36152353956560910 | 3 |
+-------------------+--------+
| 36152353956560908 | 4 |
+-------------------+--------+
| 36152353956560905 | 5 |
+-------------------+--------+
| 36152353956560902 | 6 |
+-------------------+--------+
| 36152353956560901 | 7 |
+-------------------+--------+
| 36152353956560896 | 8 |
+-------------------+--------+
| 36152353956560899 | 9 |
+-------------------+--------+
| 36152353956560900 | 10 |
+-------------------+--------+
| 36152353956560898 | 11 |
+-------------------+--------+
| 36152353956560906 | 12 |
+-------------------+--------+
| 36152353956560907 | 13 |
+-------------------+--------+
标签传播算法(lpa、lpa_u2i)
概述
LPA(Label Propagation Algorithm)是一种社区检测算法,它的核心思想是社区内部点标签的传播。该算法可以自动将具有相似特征的点聚类到一起,形成一个社区。LPA 算法的实现过程中,将每个点随机初始化为一个标签,然后在每一轮迭代中��,点将自己的标签更新为其邻居点中出现最频繁的标签。在 LPA 算法的迭代过程中,每个点都会不断地接收来自邻居点的标签信息,并不断地调整自己的标签,直到收敛为止。最终,具有相同标签的点构成一个社区。 LPA_U2I 为一种特殊图场景的实现,两种类型点 user 和 item,一种类型边。
LPA 算法可以应用于许多领域,例如社交网络分析和生物信息学。在社交网络中,LPA 算法可以帮助我们识别出具有相似兴趣爱好或社交关系的用户,并将他们划分到同一社区中。在生物信息学中,LPA 算法可以识别出同一基因家族的基因,并将它们划分到同一簇中。LPA 算法的优势在于简单易懂,迭代速度快,对于大规模数据集的处理效果尤为明显。
标签传播(LPA_U2I)仅支持一种边,两种点类型的图。
语法
MATCH ... CALL lpa($(path),$(max_round))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| max_round | int | 否 | 最大迭代轮数 | 10 |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点 ID |
| result | 点对应的社区 id |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call lpa((n)-[e]->(b), 3)
YIELD task_id
RETURN task_id; - 期望结果
+--------------------+--------------------+
| id | result |
+====================+====================+
| 36152353956560897 | 108209947994488859 |
+--------------------+--------------------+
| 36152353956560896 | 108209947994488859 |
+--------------------+--------------------+
| 36152353956560898 | 108209947994488858 |
+--------------------+--------------------+
| 36152353956560906 | 108209947994488859 |
+--------------------+--------------------+
| 36152353956560907 | 108209947994488859 |
+--------------------+--------------------+
| 108209947994488859 | 108209947994488859 |
+--------------------+--------------------+
| 108209947994488860 | 108209947994488860 |
+--------------------+--------------------+
| 108209947994488858 | 108209947994488858 |
+--------------------+--------------------+
加权标签传播(wcdlp)
概述
与标签传播算法不同的是,标签的传递跟边的权重相关,在标签传递时,每个顶点会根据标签的入边进行权重累加,在累加和最高的标签中随机选择一个。
语法
MATCH ... call wcdlp($(path), $(max_round), $(weight))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| max_round | int | 否 | 最大迭代轮数 | 10 | ||
| weight | Property | 否 | 权重属性 | e.weight |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点 ID |
| result | 点对应社区 id |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call wcdlp((n)-[e]->(b), 10, e.weight)
YIELD task_id
RETURN task_id; - 期望结果
+--------------------+--------------------+
| id | result |
+====================+====================+
| 36152353956560897 | 108209947994488859 |
+--------------------+--------------------+
| 36152353956560896 | 108209947994488860 |
+--------------------+--------------------+
| 36152353956560898 | 108209947994488858 |
+--------------------+--------------------+
| 36152353956560906 | 108209947994488860 |
+--------------------+--------------------+
| 36152353956560907 | 108209947994488860 |
+--------------------+--------------------+
| 108209947994488859 | 108209947994488859 |
+--------------------+--------------------+
| 108209947994488860 | 108209947994488860 |
+--------------------+--------------------+
| 108209947994488858 | 108209947994488858 |
+--------------------+--------------------+
监听标签传播(slpa)
概述
该算法是基于标签传播和历史标签记录的社区发现算法,是对标签传播算法的扩展。与标签传播算法不同的是,本算法会对所有顶点记录其历史标签,在迭代中对标签进行累加时,会将历史标签也计算在内。最终输出结果为每个顶点的所有历史标签记录。
对于每一个节点,每次更新时会收集邻居的标签信息,每个邻居随机选择概率正比于该标签在其存储器中的出现频率的标签,节点会将收集到出现次数最多的标签添加到历史标签中。因此如果迭代 max_round 次,则每个节点将保存一个长度为 max_round 的序列。当迭代停止后,对每一个节点历史标签序列中各(互异)标签出现的频率做统计,按照某一给定阀值r过滤掉那些出现频率小的标签,剩下的即为该节点的标签(通常有多个)。
算法 SLPA 不会像其它算法一样忘记上一次迭代中节点所更新的标签信息,它给每个节点设置了一个标签存储列表来存储每次迭代所更新的标签。最终的节点社区从属关系将由标签存储列表中所观察到的标签的概率决定,当一个节点观察到有非常多一样的标签时,那么,很有可能这个节点属于这个社区,而且在传播过程中也很有可能将这个标签传播给别的节点。更有益处的是,这种标签存储列表的设计可以使得算法可以支持划分重叠社区。
语法
MATCH ... call slpa($(path), $(max_round), $(r))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| max_round | int | 否 | 最大迭代轮数 | 10 | ||
| r | float | 否 | 用于筛选结果社区标识的阈值 | 0.3 |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点 ID |
| result | 点对应的社区 id 序列 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call slpa((n)-[e]->(b), 2, 0.3)
YIELD task_id
RETURN task_id; - 期望结果
+---------------------+---------------------+---------------------+
| 0 | | |
+=====================+=====================+=====================+
| [36152353956560897 | 36152353956560897 | 108209947994488859] |
+---------------------+---------------------+---------------------+
| [36152353956560896 | 36152353956560896 | 108209947994488859] |
+---------------------+---------------------+---------------------+
| [36152353956560898 | 36152353956560898 | 108209947994488858] |
+---------------------+---------------------+---------------------+
| [36152353956560906 | 36152353956560906 | 108209947994488859] |
+---------------------+---------------------+---------------------+
| [36152353956560907 | 36152353956560907 | 108209947994488859] |
+---------------------+---------------------+---------------------+
| [108209947994488859 | 108209947994488859] | |
+---------------------+---------------------+---------------------+
| [108209947994488860 | 108209947994488860] | |
+---------------------+---------------------+---------------------+
| [108209947994488858 | 108209947994488858] | |
+---------------------+---------------------+---------------------+
鲁汶社区(Louvain)
概述
鲁汶算法是基于模块度的社区发现算法,能够发现层次性的社区结构,其优化目标是最大化整个社区网络的模块度。
在图中点尝试遍历所有邻居的社区标签,并选择最大化模块度增量的社区标签,在最大化模块度之后,把每个社区看成一个新点,重复直到模块度不再增大。如果一个点加入到某一个社区中�会使得该社区模块度最大程度生增加,则该点就应该属于该社区;如果一个点加入到其他社区中没有引起其他社区模块度的增加,则该点留在当前社区中。
主要用于社交网虚假账号识别、消费群体划分及商品推荐、银行卡伪冒和欺诈团伙识别、银行理财产品、保险产品推荐、企业集团及家族企业识别等场景。
语法
MATCH ... call louvain(${path}, ${min_progress}, ${progress_tries} )
YIELD *
RETURN *;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| min_progress | int | 否 | 模块度增益阈值 | 10 | ||
| progress_tries | int | 否 | 多少次增益阈值不达标后退出 | 1 | ||
| weight | Property | 否 | 边上的属性字段作为权重值 | e.weight |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点 ID |
| result | 点对应的 community 值,以社区中的某一个点 id 表��示 |
示例
-
给定数据
Create graph s2(partition_num=5);
Use s2;
CREATE VERTEX person(PRIMARY KEY id String(64), name String not null);
CREATE EDGE knows
(
weight DOUBLE NOT NULL COMMENT '权重值',
FROM person TO person
);
INSERT (:person{id:'psn1', name:'aaa'}),(:person{id:'psn2', name:'bbb'}),(:person{id:'psn3', name:'ccc'}),(:person{id:'psn4', name:'ddd'}),(:person{id:'psn5', name:'fff'}),(:person{id:'psn6', name:'ggg'}),(:person{id:'psn7', name:'hhh'});
INSERT (:person{id:'psn1'})-[:knows{weight: 0.1}]->(:person{id:'psn2'});
INSERT (:person{id:'psn1'})-[:knows{weight: 0.1}]->(:person{id:'psn3'});
INSERT (:person{id:'psn1'})-[:knows{weight: 0.1}]->(:person{id:'psn7'});
INSERT (:person{id:'psn3'})-[:knows{weight: 0.1}]->(:person{id:'psn5'});
INSERT (:person{id:'psn5'})-[:knows{weight: 0.1}]->(:person{id:'psn4'});
INSERT (:person{id:'psn4'})-[:knows{weight: 0.1}]->(:person{id:'psn6'});
INSERT (:person{id:'psn4'})-[:knows{weight: 0.1}]->(:person{id:'psn5'});
INSERT (:person{id:'psn2'})-[:knows{weight: 0.1}]->(:person{id:'psn6'}); -
查询语句
MATCH (n:person)-[e:knows]->(b:person) call louvain((n)-[e]->(b), 100, 2, e.weight)
YIELD task_id
RETURN task_id; -
期望结果
+--------------------+------------------------+
| id | result |
+====================+========================+
| 36152353956560897 | 36152353956560907 |
+--------------------+------------------------+
| 36152353956560896 | 36152353956560898 |
+--------------------+------------------------+
| 36152353956560898 | 36152353956560898 |
+--------------------+------------------------+
| 36152353956560906 | 36152353956560898 |
+--------------------+------------------------+
| 36152353956560907 | 36152353956560907 |
+--------------------+------------------------+
| 108209947994488859 | 108209947994488859 |
+--------------------+------------------------+
| 108209947994488860 | 108209947994488859 |
+--------------------+------------------------+
| 108209947994488858 | 108209947994488859 |
+--------------------+------------------------+
GirvanNewman(gn)
概述
GN 图算法(Girvan-Newman algorithm)是一种用于社区发现的图分析算法,由 Mark Girvan 和 Michelle Newman 在 2002 年提出。它的主要目标是识别复杂网络中的社区结构,即将网络中的点划分为一些紧密连接的子图或社区,同时最大化社区内的连接密度,最小化社区之间的连接密度。
GN 图算法基于网络中的边介数(betweenness centrality)概念,边介数衡量了一个边在网络中的重要性,即它在网络中连接点之间的最短路径中所扮演的角色。算法的主要思想是通过计算网络中所有边的介数,然后依次删除介数最高的边,直到网络被划分为多个孤立的子图为止,因此GN算法是一种分裂算法。
语法
MATCH ... call gn($(path), $(community_count))
YIELD *
RETURN *;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示�例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| community_count | int | 否 | 期望社区数阈值 | 2 |
结果输出
| 名称 | 类型 | 描述 |
|---|---|---|
| id | string | 点 ID |
| result | int64 | 点对应的社区 id |
示例
-
给定数据
Create graph gn1(partition_num=5);
Use gn1;
CREATE VERTEX person(PRIMARY KEY id String(64), name String not null);
CREATE VERTEX post(PRIMARY KEY id String(64), name String not null);
CREATE EDGE likes
(
weight DOUBLE NOT NULL COMMENT '权重值',
FROM person TO post
);
INSERT (:person{id:'psn1', name:'aaa'}), (:person{id:'psn2', name:'bbb'}),(:person{id:'psn3', name:'ccc'});
INSERT (:post{id:'pst1', name:'d aaa'}), (:post{id:'pst2', name:'d bbb'}),(:post{id:'pst3', name:'d ccc'});
INSERT (:person{id:'psn1'})-[:likes{weight: 0.1}]->(:post{id:'pst2'});
INSERT (:person{id:'psn1'})-[:likes{weight: 0.6}]->(:post{id:'pst3'});
INSERT (:person{id:'psn2'})-[:likes{weight: 0.3}]->(:post{id:'pst2'}); -
查询语句
MATCH (n:person)-[e:likes]->(b:post) call girvan_newman((n)-[e]->(b), 3)
YIELD task_id
RETURN task_id; -
期望结果
+--------------------+--------+
| id | result |
+====================+========+
| 36152353956560897 | 0 |
+--------------------+--------+
| 36152353956560896 | 1 |
+--------------------+--------+
| 36152353956560898 | 2 |
+--------------------+--------+
| 36152353956560906 | 1 |
+--------------------+--------+
| 36152353956560907 | 1 |
+--------------------+--------+
| 108209947994488859 | 1 |
+--------------------+--------+
| 108209947994488860 | 1 |
+--------------------+--------+
| 108209947994488858 | 2 |
+--------------------+--------+
度同配系数(degree_assortativity_coefficient)
概述
计算图的度关联性。关联性度量图中连接的相似性与点度的关系。
语法
MATCH ... call degree_assortativity_coefficient($(path),$(src),$(k),$(metrics))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| source_degree_type | str | 否 | 源点的度类型(仅适用于有向图) | "out" | ||
| target_degree_type | str | 否 | 目标点的度类型(仅适用于有向图) | "in" | ||
| weighted | bool | 否 | 是否加权 | FALSE |
结果输出
| 名称 | 描述 |
|---|---|
| id | 度关联性 |
示例
- 查询语句
MATCH (n:person)-[e:knows]->(b:person) call degree_assortativity_coefficient((n)-[e]->(b), "out", "out", false)
YIELD task_id
RETURN task_id; - 期望结果
+---------------------+
| 0 |
+=====================+
| 0.11701621489018087 |
+---------------------+
平均相邻度算法(average_degree_connectivity)
概述
计算图的平均度连接性。平均度连接性是度数为 k 的点的平均最近邻的度(邻居点的度的平均值)。
语法
MATCH ... call average_degree_connectivity($(path), $(source_degree_type), $(target_degree_type))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| source_degree_type | str | 否 | 起点统计出度还是入度, “in”-,“out”- or ”in+out” | "in" | ||
| target_degree_type | str | 终点统计出度还是入度, “in”-,“out”- or ”in+out” |
结果输出
| 名称 | 描述 |
|---|---|
| 0 | 度数 |
| 1 | 平均联通度 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call average_degree_connectivity((n)-[e]->(b), "in", "out")
YIELD task_id
RETURN task_id; - 期望结果
+-----+------+
| 0 | 1 |
+=====+======+
| 4.0 | 1.75 |
+-----+------+
| 1.0 | 1.0 |
+-----+------+
| 3.0 | 2.0 |
+-----+------+
| 0.0 | 0.0 |
+-----+------+
单源点相似度(vertex_similarity_ss)
概述
给定起点,返回 top k 相似度顶点及相似值,支持 jaccard 和 common。
语法
MATCH ... call vertex_similarity_ss($(path),$(src),$(k),$(metrics))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| src | int | 否 | 起点 | 36152353956560896 | ||
| k | int | 否 | 最大跳数 | 3 | ||
| metrics | str | 否 | 度量方法,支持 common 和 jaccard 两种 | "jaccard" |
结果输出
| 名称 | 描述 |
|---|---|
| id | 目标点 id |
| result | 多少个共同邻居 |
示例
- 查询语句
MATCH (n:person)-[e:knows]->(b:person) call vertex_similarity_ss((n)-[e]->(b), 36152353956560896, 3, "common")
YIELD task_id
RETURN task_id; - 期望结果
+--------------------+------+
| 0 | |
+====================+======+
| [36152353956560896 | 3.0] |
+--------------------+------+
| [36152353956560900 | 2.0] |
+--------------------+------+
| [36152353956560897 | 1.0] |
+--------------------+------+
点相似度(vertex_similarity)
概述
判断两组点之间各个点的相似度。
语法
MATCH ... call vertex_similarity($(path),$(src),$(k),$(metrics))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| src | int | 否 | 起点 | 36152353956560896 | ||
| k | int | 否 | 最大跳数 | 3 | ||
| metrics | str | 否 | 度量方法,支持 common 和 jaccard 两种 | "jaccard" |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点配对 |
| result | 相似度 |
示例
-
查询语句
MATCH (n:person)-[e:likes]->(b:post) call vertex_similarity((n)-[e]->(b), '[36152353956560896,36152353956560901]', '[108209947994488858,108209947994488859]', "common")
YIELD task_id
RETURN task_id; -
期望结果
+--------------------+--------------------+----+
| 0 | | |
+====================+====================+====+
| [36152353956560896 | 108209947994488858 | 0] |
+--------------------+--------------------+----+
k核算法(k_core)
概述
计算每个点的核数(度数)。图的 k 核是��指在所有度数小于 k 的顶点被移除后遗留下的连通分量(其中连通分量(分量)是一个子图,其任何两个顶点通过路径可以相互连接。),用于寻找一个图中符合指定核数(度数)的顶点的集合,要求每个顶点至少与该图的其他 K 个顶点相关联。
主要适用于图推演、生物学、社交网络、金融风控等场景。
K-Core(K-核)就是所有大于等于 K 的 K-Shell 的并集。
语法
MATCH ... call k_core($(path), $(k))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| k | int | 否 | k 值, 算法判断每个点是不是属于 k 核之内 | 5 |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点 ID |
| result | 1:该点在 K-core 中, 0: 该点不在K-core中 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call kcore((n)-[e]->(b), 2)
YIELD task_id
RETURN task_id; - 期望结果
+--------------------+--------+
| id | result |
+====================+========+
| 36152353956560897 | 0 |
+--------------------+--------+
| 36152353956560896 | 1 |
+--------------------+--------+
| 36152353956560898 | 0 |
+--------------------+--------+
| 36152353956560906 | 1 |
+--------------------+--------+
| 36152353956560907 | 1 |
+--------------------+--------+
| 108209947994488859 | 0 |
+--------------------+--------+
| 108209947994488860 | 0 |
+--------------------+--------+
| 108209947994488858 | 0 |
+--------------------+--------+
k壳算法(k_shell)
概述
递归的剥离图中度数小于或等于 k 的点。假设网络中不存在度数为 0 的点。从度指标的角度分析,度数为 1 的点是图中最不重要的点,因此首先将度数为 1 的点及其边从图中删除。之后的图中会出现新的度数为 1 的点,接着将这些新出现的度数为 1 的点及其边删除。重复上述操作,直到图中不再新出现度数为 1 的点为止。此时所有被删除的点构成第一层,即 1-shell,点的 Ks 值等于 1。剩下的图中,每个点的度数至少为 2。继续重复上述删除操作,得到 Ks 值等于 2 的第二层,即 2-shell。依此类推,直到网络中所有的点都被赋予 ks 值。
语法
MATCH ... call k_shell($(path),$(k))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| k | int | 否 | 第几层 shell | 2 |
结果输出
| 名称 | 描述 |
|---|---|
| id | 点 ID(格式为“点类型:点id”) |
| result | 1: 点属于 k-shell 0: 点不属于 k-shell |
示例
-
查询语句
MATCH (n:person)-[e:likes]->(b:post) call k_shell((n)-[e]->(b), 2)
YIELD task_id
RETURN task_id; -
期望结果
+--------------------+--------+
| id | result |
+====================+========+
| 36152353956560897 | 0 |
+--------------------+--------+
| 36152353956560896 | 1 |
+--------------------+--------+
| 36152353956560898 | 0 |
+--------------------+--------+
| 36152353956560906 | 1 |
+--------------------+--------+
| 36152353956560907 | 1 |
+--------------------+--------+
| 108209947994488859 | 0 |
+--------------------+--------+
| 108209947994488860 | 0 |
+--------------------+--------+
| 108209947994488858 | 0 |
+--------------------+--------+
图模式匹配(graph_matching)
概述
根据输入的点边模式查找图中符合该模式的具体点边。
模式的表达方式:
描述一个点: {点编号},{点类型}, 如 `0,person。
描述多个点:0,{点 0 类型};1,{点 1 类型}; ... n,{点 n 类型}可以表述成 "0,person;1,post"。
描述一条边: {起点编号},{终点编号},{边类型}。
描述多条边: {边 0 起点编号},{边 0 终点编号},{边 0 类型};{边 1 起点编号},{边 1 终点编号},{边 1 类型};....{边 n 起点编号},{边 n 终点编号},{边n类型}。
语法
MATCH ... call graph_matching($(path),$(limit),$(vertices),$(edges))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| limit | int | 否 | 返回数量限制 | 3 | ||
| vertices | str | 否 | 点与其 type 之间以英文逗号分隔,各点与其 type 对之间以换行符“;”分隔 | “0,person;1,post;2,person” | ||
| edges | str | 否 | 边的起点与终点之间以英文逗号分隔,各边之间以换行符“;”分隔。 | “0,1,knows;1,2,beliked” |
结果输出
| 名称 | 描述 |
|---|---|
| 0 | 符合模式的点边 |
示例
- 查询语句
MATCH (n:person)-[e:knows]->(b:person) call graph_matching((n)-[e]->(b),3,"0,person;1,person;2,person","0,1,knows;2,1,knows")
YIELD task_id
RETURN task_id; - 期望结果
+--------------------+--------------+--------------------+--------------+--------------------+--------------+--------------------+------------------+-----------+-----+--------------------+------------------+-----------+-----+
| 0 | 1 | 2 | 3 | 4 | | | | | | | | | |
+====================+==============+====================+==============+====================+==============+====================+==================+===========+=====+====================+==================+===========+=====+
| "[36152353956560896 | \"person\"]" | "[36152353956560898 | \"person\"]" | "[36152353956560897 | \"person\"]" | "[36152353956560897 | 36152353956560898 | \"knows\" | 0]" | "[36152353956560896 | 36152353956560898 | \"knows\" | 0]" |
+--------------------+--------------+--------------------+--------------+--------------------+--------------+--------------------+------------------+-----------+-----+--------------------+------------------+-----------+-----+
环路检测(cycle_detection)
概述
返回图内所有k跳以内的环路。
语法
MATCH ... call cycle_detection($(path),$(limit),$(khop))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| limit | int | 否 | 结果循环限制 | 3 | ||
| khop | in t | 否 | k-hop数量限制 | 4 |
结果输出
| 名称 | 描述 |
|---|---|
| 0 | 点类型 |
| 1 | 点ID |
| 2 | 边类型 |
| 3 | 边rank |
| 4 | 点类型 |
| 5 | 点ID |
| ... | ... |
示例
-
查询语句
MATCH(n:person)-[e:knows]->(b:person) call cycle_detection((n)-[e]->(b), 3, 4)
YIELD task_id
RETURN task_id; -
期望结果
+--------+-------------------+-------+---+--------+-------------------+-------+---+--------+-------------------+-------+----+--------+-------------------+-------+----+
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
+========+===================+=======+===+========+===================+=======+===+========+===================+=======+====+========+===================+=======+====+
| person | 36152353956560897 | knows | 0 | person | 36152353956560898 | knows | 0 | person | 36152353956560900 | knows | 0 | person | 36152353956560896 | knows | 0 |
+--------+-------------------+-------+---+--------+-------------------+-------+---+--------+-------------------+-------+----+--------+-------------------+-------+----+
EgoNet算法(ego_net)
概述
EgoNet 算法是一种基于根顶点的子图挖掘算法,它的目标是找到根顶点周围的邻居点,并以根顶点为中心构建一个包含根顶点及其K度以内邻居点的子图,该子图被称为根顶点的EgoNet。
EgoNet 算法可以用于分析社交网络中个人的关系和邻居结构。通过构建EgoNet子图,可以研究个人的朋友、亲属、合作伙伴等关系,并对个人的影响力、信息传播等进行分析。在基于用户的推荐系统中,EgoNet算法可以用于生成用户的个人兴趣网络,从而提供个性化的推荐。通过构建用户的EgoNet子图,可以发现用户的兴趣点、兴趣群体等信息,为用户提供更精准的推荐结果。在网络安全领域,EgoNet算法可以用于识别潜在的恶意点或者攻击路径。通过分析网络中点的EgoNet子图,可以发现点的连接模式、关键点以及异常行为,从而提供网络安全的决策依据。
语法
MATCH ... call ego_net($(path), $(src), $(k))
YIELD task_id
RETURN task_id;
参数说明
| 名称 | 类型 | 规范 | 默认 | 可选 | 描述 | 示例 |
|---|---|---|---|---|---|---|
| path | Path | 否 | 路径,描述一个联通子图 | (n)-[e]-(b) | ||
| src | int | 否 | 中心点 | 36152353956560896 | ||
| k | int | 否 | 最大跳数 | 3 |
示例
- 查询语句
MATCH (n:person)-[e:likes]->(b:post) call ego_net((n)-[e]->(b), 36152353956560896, 3)
YIELD task_id
RETURN task_id; - 期望结果
+--------------------+---------+---+---------------------+
| 0 | | | |
+====================+=========+===+=====================+
| [36152353956560896 | "likes" | 0 | 108209947994488859] |
+--------------------+---------+---+---------------------+
| [36152353956560896 | "likes" | 0 | 108209947994488860] |
+--------------------+---------+---+---------------------+
自定义算法
ArcGraph 图数据库中的 ArcGraph OLAP 引擎内置了多种先进的图算法,为用户提供强大的数据处理能力。同时,为了满足不同业务场景的特定需求,ArcGraph OLAP 引擎还允许用户自行开发自定义算法。在深入介绍算法开发之前,我们需要先了解一些基本概念与框架。
核心概念
我们将以图 G 为例介绍开发自定义算法所涉及的一些基本概念。
-
子图(Fragment)
在算法执行前需要先加载图的数据,对于大规模图数据,ArcGraph 图数据库采用分布式集群加载策略,将图按点和边的数量尽可能均匀切分为多个不同的子图(Fragment),并分发至集群中不同的服务器节点进行加载处理。如图 G 所示,图 G 被切分为“F0”、“F1”、“F2”等三个子图。 -
内部点(InnerVertex)与外部点(OuterVertex)
在 ArcGraph 图数据库中,根据点与子图的关联关系,图中的点被划分为内部点(InnerVertex)和外部点(OuterVertex)。- 内部点(InnerVertex):是指完全属于某个子图的点。如在图 G 中的点“0”、点“6”等完全位于其所属子图内的点,均被视为内部点。
- 外部点(OuterVertex):是指在一个子图内,但同时与其他子图中的点存在连接关系的点。当某条边连接的两个点分属不同子图时,为了计算方便,会在相关的子�图中都保留这个点的副本,即“镜像点”。例如,在图 G 中,点“1” 和点“3”虽属于“F0”子图,但在“F1”子图中也会有对应的副本,所以对于“F1”子图来说,这 2 个点就是外部点。请注意,外部点只参与子图的局部计算,最终的结果还需要同步到该点所属的子图进行计算。
PIE 编程模型
在图计算中,算法的框架遵循 PIE(PEval-IncEval-Assemble)编程模型。该模型将算法的执行过程划分为 PEval、IncEval 和 Assemble 三个核心阶段。每个算法都需要提供这三个部分的代码,然后由算法框架进行并行计算,算法的执行过程中服务器节点间会通过消息传递机制进行消息和数据的同步。
三个阶段的详细说明如下:
- PEval 阶段
PEval 阶段主要负责局部数据的初始计算。该阶段通常在单机环境下运行,且多数情况下仅需执行一次。 - IncEval 阶段
IncEval 阶段是算法的核心部分,涉及在每个服务器节点上进行迭代计算,每一次迭代被称为一个超步(superstep)计算。在迭代过程中服务器节点间通过消息传递机制同步中间结果。 - Assemble 阶段
Assemble 阶段用于收集并汇总每个服务器节点的部分结果,得到最终结果。
算法框架
ArcGraph 图数据库在进行图计算操作时,图的加载、子图生成、算法的加载与执行、服务器节点间的消息传递和同步等核心操作都是由 ArcGraph OLAP 引擎完成。以下将详细介绍算法执行过程中涉及的主要组件以及实现自定义算法的方式。

主要组件
- Fragment:子图组件,负责对图中点和边的访问。
- Message Manager:消息管理组件,负责服务器节点间消息的传递以及状态的同步。
- Worker:工作组件,负责算法执行的具体流程,包括加载 Fragment、加载算法、执行算法、服务器节点间通信、结果处理等。
- Application(App):算法的 App 组件,是算法的主要逻辑部分。可以访问本地的 Fragment,并通过 Message Manager 与其他服务器节点进行交互。
- Context:算法的上下文(Context)组件,用于管理算法的参数和结果。
算法实现
在实现算法时,只需要按照规范实现其中的 Context 和 Application(App)两个组件即可。其中,Context 组件可以继承自 VertexDataContext 或 TensorContext;App 组件继承自 AppBase 或 ParallelAppBase,还可以根据需要继承 Communicator、ParallelEngine 等类,以实现通信和并发处理。
算法的核心在于 App 组件,它按照 PIE 编程模型进行调度,需要实现 PEval 和 IncEval 两个方法。其中,PEval 负责每个服务器节点的局部计算,通常完成分区后的初始计算;而 IncEval 负责在每个服务器节点上完成每一次超步的计算,并在服务器节点之间同步中间结果。虽然 App 组件中并没有明显的 PIE 模型中的 Assemble 阶段,但在满足迭代终止条件时,通常会在 IncEval 中完成结果的整合与汇总。
算法执行框架
ArcGraph 图数据库的自定义算法执行框架,可参考如下伪代码,这部分代码属于 ArcGraph OLAP 引擎中的算法执行框架。在框架中,每个服务器节点依据加载的图类型和算法类型动态生成 worker 对象,且 worker 对象的 Query 方法会执行包括调用算法的 PEval 方法和 IncEval 方法在内的完整算法流程,直至满足结束条件。在循环调用过程中每一次对 IncEval 的调用都叫做一次超步。
Query(args) {
MPI_Barrier(comm_spec_.comm());
context_->Init(messages_, args);
round = 0;
messages_.Start();
messages_.StartARound();
app_->PEval(*graph_, *context_, messages_);
messages_.FinishARound();
step = 1;
while (!messages_.ToTerminate()) {
round++;
messages_.StartARound();
app_->IncEval(*graph_, *context_, messages_);
messages_.FinishARound();
++step;
}
MPI_Barrier(comm_spec_.comm());
messages_.Finalize();
}
在 ArcGraph 图数据库中,自定义算法是通过开源的并行计算库 OpenMPI 进行并行计算的。关于算法执行过程中几个关键特性的详细说明如下:
MPI_Barrier:表示集群中所有的服务器节点要在这个位置等待其他服务器节点也执行到该位置,实现执行同步。messages_:调用 OpenMPI 的各类消息传递函数实现服务器节点间的消息传递。messages_.ToTerminate():用于判断算法是否达到结束条件。当任意一个服务器节点调用 ForceTerminate 方法,或所有服务器节点均无待发送消息且均未调用 ForceContinue 方法时,表明算法可以正常结束。
快速入门
ArcGraph 图数据库支持以 Java、C++ 和 Python 语言进行自定义算法开发。本章节将以 Java 语言为例,详细介绍在 ArcGraph 图数据库中如何进行自定义算法开发。
准备开发环境
在进行自定义算法开发操作前请确认您已经成功部署单机版或敏捷版 ArcGraph 图数据库中的 ArcGraph OLAP 引擎。部署完成后,您可以在任意一个服务器节点上进行自定义算法的开发。
算法的开发、编译和测试需要在服务器节点的容器内进行。使用以下命令进入容器,后续操作(如创建项目、编译和测试等)均在此容器中进行。
语法
docker exec -it <engine_name> bash
详细说明
<engine_name>:指定用于算法开发时服务器节点的容器名称。
示例
在 ArcGraph OLAP 引擎中的服务器节点(容器名称为“engine-0”)的命令行终端中执行如下命令进入对应容器:
docker exec -it engine-0 bash
创建项目
通过命令行工具创建算法项目并生成项目模板。操作前确保您已进入到服务器节点对应的容器环境中,并具备执行命令行操作的权限。
语法
fabarta-cli app new <app_name> --app-type=<java|cpp|python> --output=<dir_name>
详细说明
<app_name>:指定算法名称。自定义算法名称,需确保在同一个 ArcGraph 集群中唯一并遵循特定的命名规则,详情请参见 命名规则 章节。--app-type:指定算法类型,支持 Java、C++ 和 Python 三种类型。--output:指定项目目录,即算法存放路径,可在执行命令时自动创建该路径。
示例
在容器内执行以下命令,可在“traverse”目录下创建名为“traverse”的 Java 算法项目:
fabarta-cli app new traverse --app-type=java --output=traverse
不同的算法类型生成的项目代码文件不同,请以实际为准。以 Java 算法项目为例,生成的文件清单如下:
├── assembly.xml
├── pom.xml
├── README.md
├── .gs_conf.yaml
├── traverse.py
├── src
│ └── main
│ └── java
│ └── com
│ � └── fabarta
│ └── example
│ ├── TraverseContext.java
│ └── Traverse.java
├── target
......
│ ├── traverse-example-0.27.0.jar
│ └── traverse-example-assemble.zip
文件清单说明
- pom.xml 和 assembly.xml
pom.xml 文件用于算法的编译和打包,可在该文件中配置算法的 .jar 包名称及版本;assembly.xml 文件包含 pom.xml 的打包逻辑,除了打包 .jar 文件�之外,还会生成一个 .zip 文件(需手动重命名为 .gar)用于后续的算法注册。 - .gs_conf.yaml
算法配置文件,在创建算法项目时自动生成,一般情况下不需要修改。 - traverse.py
算法签名文件,包含注册算法所需要的算法名、算法参数及类型等信息。在创建算法项目时自动生成,需要根据算法的具体情况更新。 - TraverseContext.java 和 Traverse.java
分别是算法的 Context 类和 App 类文件。文件名根据创建算法项目时指定的算法名以“underscore_to_camelcase”的规则自动生成,类名与文件名一致。具体的规则是生成的类名以大写字母开始,算法名中下划线之后的字母会转换成大写字母。默认的算法包名为“com.fabarta.example”,可根据需要调整目录结构以改变算法包名称。 - target
target 目录下是 Maven 编译打包后的结果,其中 traverse-example-assemble.zip 是算法注册需要的打包文件,它包含了算法配置文件 .gs_conf.yaml、算法签名文件 traverse.py 和算法包 traverse-example-0.27.0.jar。
编译和打包
Java 语言
以 Java 语言进行算法开发时,当算法项目创建完成后,进入项目的根目录,并执行如下 Maven 命令进行编译和打包。编译结果将存储在“target”目录下,以 .jar 文件形式呈现。
mvn clean package
示例
创建算法名为“traverse”的项目之后,在容器中运行以下命令,进入项目的根目录(“traverse”)并进行编译和打包:
#进入traverse根目录中
cd traverse
#编译和打包
mvn clean package
生成的结果为“./target/traverse-example-0.27.0.jar”,项目的版本号是 0.27,在 pom.xml 文件中可修改版本号。
Python 语言
以 Python 语言进行算法开发时,当算法项目创建完成后,使用如下命令执行源代码:
python3 my_traverse.py package
命令执行成功后,将生成一个名为“traverse.gar”的 gzip 压缩包,该压缩包内含算法的项目代码文件,解压后可查看算法文件。
测试
算法打包完成后,可以使用测试脚本来验证其功能。
测试脚本
以下是一个简单的测试脚本示例:
import arcgraph
from arcgraph import JavaApp
from arcgraph.dataset import load_p2p_network
from arcgraph.framework.app import load_app
arcgraph.set_option(show_log=True)
arcgraph.set_option(log_level="DEBUG")
sess = arcgraph.session(cluster_type='hosts')
graph = load_p2p_network(sess)
graph = graph.project(vertices={"host": ['id']}, edges={"connect": ["dist"]})
sess.add_lib("./target/traverse-example-0.27.0.jar")
app=load_app(algo="java_pie:com.fabarta.example.Traverse")
ctx=app(graph._project_to_simple(e_prop = 'dist', v_prop='id'), maxIteration=1)
print(ctx.to_numpy("r"))
脚本说明
sess = arcgraph.session(cluster_type='hosts'):创建会话并指定会话模式,支持单机模式、集群模式等多种会话模式。其中,cluster_type='hosts'表示会话模式为单机模式。创建会话后自动启动会话模式需要的进程,包括执行算法所需要的引擎,测试脚本结束时这些进程会自动退出。graph = load_p2p_network(sess):加载图数据,数据会尽可能均匀的切分成子图并加载到不同的服务器节点上,由于示例使用的是单机模式,所以整个图数据都会加载到本地。其中,load_p2p_network(sess)表示加载内置的“p2p_network”图数据,也可以加载其他内置图数据,或者通过load_graph方法加载指定的 csv 文件。graph = graph.project(vertices={"host": ['id']}, edges={"connect": ["dist"]}):按需裁剪图数据,设置需保留的点边属性。其中,vertices={"host": ['id']}, edges={"connect": ["dist"]}表示保留host点中的id字段,以及connect边中的dist属性。sess.add_lib("./target/traverse-example-0.27.0.jar"):加载算法.jar 包文件。加载算法 .jar 包文件到系统路径下,需要指定 .jar 包的存放位置,默认是在“target”目录下。app=load_app(algo="java_pie:com.fabarta.example.Traverse"):加载 .jar 包里的算法,生成 App 对象。其中,algo参数中java_pie表示这是一个 Java 实现的算法,com.fabarta.example.Traverse指的是算法的类名。ctx=app(graph._project_to_simple(e_prop = 'dist', v_prop='id'), maxIteration=1):执行算法。其中,第一个参数是_project_to_simple之后的图对象,随后跟随的是算法所需的参数,如果算法支持更多参数,请依次添加至其后即可。print(ctx.to_numpy("r")):输出最终的结果数据。其中,selector参数用于结果的过滤,一般使用“r”表示输出所有的结果。
执行测试脚本
将测试脚本保存为 .py 文件(如命名为“test.py”),并放入项目根目录下。进入项目根目录,执行以下命令运行测试脚本:
python test.py
执行过程中将输出大量日志信息,测试完成后,返回数组结果示例如下:
......
[100 99 92 ... 72 3 43]
......
部署算法
在部署图算法时,本地测试与正式环境操作流程不同。本地测试时可以直接加载 .jar 文件运行算法,而正式环境则需要先注册算法,并在调用算法时实时编译执行。请注意,算法注册时需要将 Maven 打包时生成的 .zip 文件后缀改成 .gar。
算法注册
通过调用图计算服务的 API 接口注册算法。请将准备好的 .gar 文件放置在执行 curl 命令的当前目录后使用以下命令进行注册:
curl -X 'POST' \
'http://127.0.0.1:18000/graph-computing/apps/gar?project_id=abc&app_name=Traverse' \
-H 'accept: application/json' \
-H 'Content-Type: multipart/form-data' \
-F 'uploaded_file=@traverse.gar'
算法运行
支持通过平台运行、调用 API 运行和 Client 调用三种方式运行算法,以满足不同用户的需求。
- 平台运行
在 ArcGraph 图开发平台上,可以直接运行已注册的算法,详情请参见《ArcGraph 图平台用户手册》。 - 调用API运行
若选择直接调用图计算服务的 API 接口运行算法,可参考以下命令示例进行操作:curl -X 'POST' \
'http://127.0.0.1:18000/graph-computing/?project_id=abc&use_cache=true&reload=false' \
-H 'accept: application/json' \
-H 'Content-Type: application/json' \
-d '{
"algorithmName": "Traverse",
"graphName": "p2p_network",
"taskId": "test_java",
"subGraph": {
"edgeTypes": [
{
"edgeTypeName": "knows",
"vertexPairs": [
{
"fromName": "person",
"toName": "person"
}
],
"props": ["dist"]
}
],
"vertexTypes": [
{
"vertexTypeName": "person",
"props": ["weight"]
}
]
},
"algorithmParams": {
"maxIteration" : 1
}
}' - Client 调用
如上述在测试算法的 test.py 中所使用的方式。Client 调用方式只限于在本地测试算法,不建议应用于正式环境。
Java 图算法开发
ArcGraph 图数据库支持用户根据实际情况以 Java 语言开发和运行图算法。
环境准备��
请确保已经成功部署 ArcGraph 图数据库中的 ArcGraph OLAP 引擎。图算法的开发与运行应直接在 ArcGraph OLAP 引擎内进行,无需额外配置 Java 或其他外部环境。
概念说明
数据结构
Vertex

Vertex 定义一个点,除了一个 value 属性用于保存点的 ID 以外,并没有保存其他数据。由于内部点的 ID 是自增的数字,所以可以通过定义 ++、-- 操作实现点的自增和自减,也可以定义 + 操作符实现点增加偏移量的操作。
Java 使用示例:
import com.alibaba.graphscope.ds.Vertex;
VertexRange
VertexRange 定义一个指定数据类型(如 long)的范围,主要用于遍历点的列表。在子图内部,点的 ID 通常是自增的,因此可以直接使用 int64_t 作为遍历的索引。由于点的内部 ID 是自增的,所以可以指定 begin 和 end 来表示点的范围,VertexRange 只需要判断点的 ID 是否在 begin 和 end 之间即可判断一个点是否包含在列表中。VertexRange 内部仅保存起始(begin)和结束(end),并且实现遍历所需的一系列方法,从而以极小的��代价实现对点列表的遍历。如上图所示的 begin 和 end 以虚线形式指向一个列表,表示 VertexRange 能够遍历从 begin 到 end 之间的点列表,但 VertexRange 本身并不直接存储这些点的具体列表。
Java 使用示例:
import com.alibaba.graphscope.ds.VertexRange;
VertexArray
VertexArray 是一个用于存储图中点及其值的列表结构,通常使用 VertexArray 保存算法的计算结果。VertexArray 会分配一块大小为“(end-begin)*sizeof(long) ”的内存,base 指针会指向这块内存的首地址。这块内存区域可以视作一个数组,其中每个元素对应 begin 到 end 范围内的一个点,且每个点在数组中有一项,用来保存点绑定的值(通常是算法的计算结果)。
VertexArray 内部包含 VertexRange 的成员 range,用于保存 begin 和 end。fake_start 是一个虚拟的开始位置,其实际值为 base-begin。如果全量的点是一个列表,那么 fake_start 会指向这个列表的首地址,通过 fake_start 可以更方便进行数据的操作,例如通过 fake_start[id] 可以直接访问 ID 为 id 的点数据的位置。
VertexArray 包含一下主要方法:
void Init(const VertexRange<VID_T>& range): 初始化指定点列表。void Init(const VertexRange<VID_T>& range, const T& value): 初始化指定点列表并设置初始值。void SetValue(VertexRange<VID_T>& range, const T& value): 为指定点列表中的点赋值。void SetValue(const Vertex<VID_T>& loc, const T& value): ��为指定点赋值。void SetValue(const T& value): 为当前所有点赋值。void Clear(): 清空点列表。const VertexRange<VID_T>& GetVertexRange(): 返回点列表。
Java 使用示例:
import com.alibaba.graphscope.ds.GSVertexArray;
VertexSet
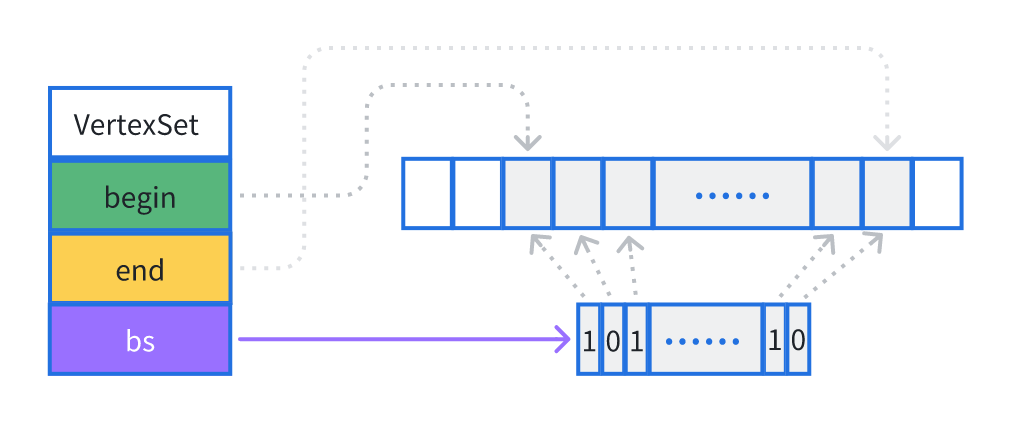
VertexSet 内部采用 bitmap 作为其底层成员 bs,为范围内的每个点分配一个布尔值。它通常通过 VertexRange 对象或 begin 和 end 参数进行初始化,主要用于在遍历 VertexRange 过程中过滤特定点。
Java 使用示例:
import com.alibaba.graphscope.ds.VertexSet;
IntArrayWrapper
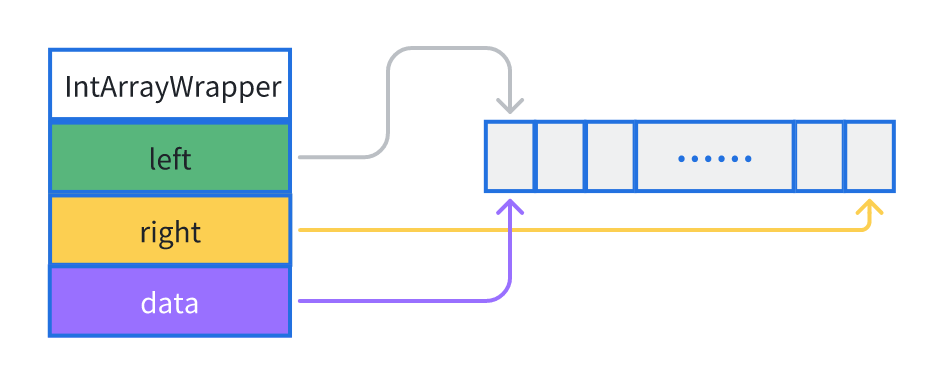
IntArrayWrapper 实现的功能与 int 数组类似,它可以与 VertexRange 协同工作,实现与 VertexArray 一样的功能。它包含 left、right(相当于 VertexRange 的 begin 和 end)和 data(用于指向 INT 数组,大小为 right - left)等三个成员。
通过 VertexRange 初始化 IntArrayWrapper,用于遍历特定范围的点。或者使用 frag.getInnerVerticesNum() 初始化 IntArrayWrapper,可以遍历整个内部点并为每个点保存值(如出度),如 Context 中定义的 degree 就是使用该方法进行初始化并保存点的出度值。
IntArrayWrapper 包含以下方法:
//构造函数
IntArrayWrapper()
IntArrayWrapper(int s, int defaultValue)
IntArrayWrapper(VertexRange<Long> vertices, int defaultValue)
//获取点绑定的值
int get(int ind)
int get(long ind)
int get(Vertex<Long> vertex)
//设置点绑定的值
void set(long ind, int newValue)
void set(int ind, int newValue)
void set(Vertex<Long> vertex, int newValue)
void set(int newValue)
//返回数组大小
int getSize()
Java 使用示例:
import com.alibaba.graphscope.utils.IntArrayWrapper;
LongArrayWrapper
LongArrayWrapper 与 IntArrayWrapper 在功能上极为相似,唯一的区别在于它内部的数据成员(data)是一个 long 类型的数组,用于存储长整型数据。
Java 使用示例:
import com.alibaba.graphscope.utils.LongArrayWrapper;
类型
Fragment
Fragment 在图算法中表示子图对象,对图中点和边的访问都需要通过 Fragment 对象完成。在算法执行过程中,如 PEval、IncEval、Output 等方法通常都会有一个 IFragment 类型的参数,以实现对图数据的操作。加载的图数据结构和需求不同,Fragment 对象的实际类型会有所不同,常用的 Fragment 类型有 ArrowProjectedFragment 和 ArrowFlattenedFragment,但算法开发者无需关心其具体类型,因为所有 Fragment 类型都会实现 IFragment 接口中的方法。
IFragment 接口中的常用方法有:
- 获取
vertex_range_t类型的点列表//获取全部点
VertexRange<VID_T> vertices()
//获取内部点
VertexRange<VID_T> innerVertices()
//获取外部点
VertexRange<VID_T> outerVertices() - 获取单个点
//是否内部点
boolean isInnerVertex(Vertex<VID_T>)
//是否外部点
boolean isOuterVertex(Vertex<VID_T>)
//oid是否存在,不存在返回false,存在则获取点的内部id,并返回true
boolean getVertex(OID_T, Vertex<VID_T>)
//oid是否存在并且是内部点,不满足条件返回false,满足则获取点的内部id,并返回true
boolean getInnerVertex(OID_T, Vertex<VID_T>)
//oid是否存在并且是外部点,不满足条件返回false,满足则获取点的内部id,并返回true
boolean getOuterVertex(OID_T, Vertex<VID_T>)
//获取点上的数据
VDATA_T getData(Vertex<VID_T>)
//设置点上的数据
void getData(Vertex<VID_T>, VDATA_T) - 获取 id 并转换
//gid转成vertex
boolean gid2Vertex(VID_T, Vertex<VID_T>)
//vertex转成gid
VID_T vertex2Gid(Vertex<VID_T>)
//获取点的oid
OID_T getId(Vertex<VID_T>)
//获取内部点的oid
OID_T getInnerVertexId(Vertex<VID_T>)
//获取外部点的oid
OID_T getOuterVertexId(Vertex<VID_T>)
//gid转成vertex,如果点存在并且是内部点返回true,否则返回false
boolean innerVertexGid2Vertex(VID_T, Vertex<VID_T>)
//gid转成vertex,如果点存在并且是外部点返回true,否则返回false
boolean outerVertexGid2Vertex(VID_T, Vertex<VID_T>)
//内部点vertex转成gid
VID_T getOuterVertexGid(Vertex<VID_T>)
//外部点vertex转成gid
VID_T getInnerVertexGid(Vertex<VID_T>) - 获取点和边的数量
//获取内部点数量
long getInnerVerticesNum()
//获取外部点数量
long getOuterVerticesNum()
//获取点数量
long getVerticesNum()
//获取边数量
long getEdgeNum()
//获取入边数量
long getInEdgeNum()
//获取出边数量
long getOutEdgeNum()
//获取整个图点的数量
long getTotalVerticesNum() - 获取邻边
//获取点的入边列表
AdjList<VID_T, EDATA_T> getIncomingAdjList(Vertex<VID_T>)
//获取点的出边列表
AdjList<VID_T, EDATA_T> getOutgoingAdjList(Vertex<VID_T>)
MessageManager
在图算法中 MessageManager 主要用于各点之间的消息传递和管理。
//找到点的所有出边的邻点所在的子图列表,对这些子图发指定消息
boolean sendMsgThroughOEdges(IFragment, Vertex, MSG_T, int channelId)
//找到点的所有边的邻点所在的子图列表,对这些子图发指定消息
boolean sendMsgThroughEdges(IFragment, Vertex, MSG_T, int channelId)
//找到点的所有入边的邻点所在的子图列表,对这些子图发指定消息
boolean sendMsgThroughIEdges(IFragment, Vertex, MSG_T, int channelId)
//针对上一个超步收到的消息进行处理
void parallelProcess(IFragment, int threadNum, ExecutorService, Supplier<MSG_T>, BiConsumer)
ParallelEngine
在图算法中 ParallelEngine 主要用于提供一些并发的操作功能。
-
forEachVertex
forEachVertex在ParallelEngine中拥有多个版本,每个版本参数各异,旨在并发的遍历点列表并对符合条件的点执行BiConsumer类型的consumer定义操作。其中,vertices参数指定点范围;threadNum和ExecutorService设定并发度。若提供了vertexSet参数,则会用vertexSet过滤点,且仅对vertexSet中存在的点执行consumer操作。void forEachVertex(VertexRange<Long> vertices, int threadNum, ExecutorService executor, BiConsumer<Vertex<Long>, Integer> consumer);
<MSG_T extends PrimitiveMessage> void forEachVertex(VertexRange<Long> vertices, int threadNum, ExecutorService executor, VertexSet vertexSet, TriConsumer<Vertex<Long>, Integer, PrimitiveMessage> consumer, Supplier<MSG_T> msgSupplier);
void forEachVertex(VertexRange<Long> vertices, int threadNum, ExecutorService executor, VertexSet vertexSet, BiConsumer<Vertex<Long>, Integer> consumer)
Communicator
在图算法中 Communicator 是一个负责处理图数据通信和交互的组件,主要用于优化图数据的传输、同步和交互过程。
//底层通过OpenMPI的消息发送和接收实现所有节点的msgIn汇总后保存到主节点的msgOut
<MSG_T> void sum(MSG_T msgIn, MSG_T msgOut)
//取所有节点的msgIn变量的最小值存到主节点的msgOut
<MSG_T> void min(MSG_T msgIn, MSG_T msgOut)
//取所有节点的msgIn变量的最大值存到主节点的msgOut
<MSG_T> void max(MSG_T msgIn, MSG_T msgOut)
应用示例
为展示图算法的实际应用,我们将探讨一个更为复杂的例子:Pagerank算法。
Pagerank 算法,即网页排名算法,是由 Google 的佩奇和布林在 1997 年提出的链接分析算法。Pagerank 算法通过增加网页质量的属性,综合考虑链接到网页的数量以及链接来源网页的质量来评估网页的重要性,有效防止了通过创建大量无用链接来提升网页排名的行为,确保网页排名的公正性和准确性。
Context 类
Context 类的 Init 方法主要负责执行初始化和参数解析操作。对于 Pagerank 算法,其参数模型模拟了用户在网页浏览时的行为,即用户可能随机点击当前网页的任一链接,也有一定概率直接跳转至其他网页。其中,alpha 参数定义了用户继续访问当前网页中某个链接的概率,即沿着当前点的某个出边继续进行遍历的概率,默认值为 0.85;而 maxIteration 参数则指定了算法的最大迭代次数。此外,threadNum 参数用于指定算法执行时的线程数量,默认值为 1。
Context 类的 Output 方法用于执行额外的结果处理操作。默认情况下,Output 方法可以留空,此时算法框架将自动输出 data 对象的内容作为最终结果。PageRankContext 继承自 VertexDataContext,VertexDataContext 类预定义了一个可通过 data() 方法获取的 data 对象。为存储 PageRank 计算结果,我们定义了 GSVertexArray<Long> 类型的 pagerank 对象,并在 Init 方法中将其初始化为 data 对象,从而确保对 pagerank 的操作即是对 data 的操作。在结果处理时,系统将直接输出 data 的内容,因此,只需确保 data(即 pagerank)对象保存了预期的计算结果即可。
Context 类中定义的其他属性将作为辅助变量在后续 App 类部分中详细说明其用法。
具体代码示例如下:
package com.fabarta.example.pagerank;
import com.alibaba.fastjson.JSONObject;
import com.alibaba.graphscope.context.ParallelContextBase;
import com.alibaba.graphscope.context.VertexDataContext;
import com.alibaba.graphscope.ds.Vertex;
import com.alibaba.graphscope.ds.VertexRange;
import com.alibaba.graphscope.fragment.IFragment;
import com.alibaba.graphscope.parallel.MessageInBuffer;
import com.alibaba.graphscope.parallel.ParallelMessageManager;
import com.alibaba.graphscope.utils.DoubleArrayWrapper;
import com.alibaba.graphscope.utils.FFITypeFactoryhelper;
import com.alibaba.graphscope.utils.IntArrayWrapper;
import org.slf4j.Logger;
import org.slf4j.LoggerFactory;
import java.io.BufferedWriter;
import java.io.File;
import java.io.FileWriter;
import java.io.IOException;
import java.util.concurrent.ExecutorService;
import java.util.concurrent.Executors;
public class PageRankContext extends VertexDataContext<IFragment<Long, Long, Long, Double>, Double>
implements ParallelContextBase<Long, Long, Long, Double> {
private static Logger logger = LoggerFactory.getLogger(PageRankContext.class);
public double alpha;
public int maxIteration;
public int superStep;
public double danglingSum;
public GSVertexArray<Long> pagerank;
public DoubleArrayWrapper nextResult;
public IntArrayWrapper degree;
public int thread_num;
public ExecutorService executor;
public MessageInBuffer.Factory bufferFactory;
public int chunkSize;
public double sumDoubleTime = 0.0;
public double swapTime = 0.0;
public int danglingVNum;
@Override
public void Init(
IFragment<Long, Long, Long, Double> frag,
ParallelMessageManager javaParallelMessageManager,
JSONObject jsonObject) {
createFFIContext(frag, Double.class, false);
if (!jsonObject.containsKey("alpha")) {
logger.error("expect alpha in params");
return;
}
alpha = jsonObject.getDouble("alpha");
if (!jsonObject.containsKey("maxIteration")) {
logger.error("expect alpha in params");
return;
}
maxIteration = jsonObject.getInteger("maxIteration");
if (!jsonObject.containsKey("threadNum")) {
logger.warn("expect threadNum in params");
thread_num = 1;
} else {
thread_num = jsonObject.getInteger("threadNum");
}
bufferFactory = FFITypeFactoryhelper.newMessageInBuffer();
logger.info(
"alpha: ["
+ alpha
+ "], max iteration: ["
+ maxIteration
+ "], thread num "
+ thread_num);
pagerank = data();
nextResult = new DoubleArrayWrapper((int) frag.getInnerVerticesNum(), 0.0);
degree = new IntArrayWrapper((int) frag.getInnerVerticesNum(), 0);
executor = Executors.newFixedThreadPool(thread_num());
chunkSize = 1024;
danglingVNum = 0;
}
@Override
public void Output(IFragment<Long, Long, Long, Double> frag) {
String prefix = "/tmp/pagerank_parallel_output";
logger.info("sum double " + sumDoubleTime / 10e9 + " swap time " + swapTime / 10e9);
String filePath = prefix + "_frag_" + String.valueOf(frag.fid());
try {
FileWriter fileWritter = new FileWriter(new File(filePath));
BufferedWriter bufferedWriter = new BufferedWriter(fileWritter);
VertexRange<Long> innerNodes = frag.innerVertices();
Vertex<Long> cur = FFITypeFactoryhelper.newVertexLong();
for (long index = 0; index < frag.getInnerVerticesNum(); ++index) {
cur.setValue(index);
Long oid = frag.getId(cur);
bufferedWriter.write(
cur.getValue() + "\t" + oid + "\t" + pagerank.get(index) + "\n");
}
bufferedWriter.close();
} catch (IOException e) {
e.printStackTrace();
}
}
public int thread_num() {
return thread_num;
}
}
App 类
App 类定义了 PEval 和 IncEval 两个关键方法。当开始执行算法时,每个服务器节点上的 Worker 会首先执行 PEval 方法进行初始化,随后进入迭代过程,其中每个超步都会调用一次 IncEval,直至满足算法的终止条件。
具体代码示例如下:
package com.fabarta.example.pagerank;
import com.alibaba.graphscope.app.ParallelAppBase;
import com.alibaba.graphscope.communication.Communicator;
import com.alibaba.graphscope.context.ParallelContextBase;
import com.alibaba.graphscope.ds.Vertex;
import com.alibaba.graphscope.ds.VertexRange;
import com.alibaba.graphscope.ds.adaptor.AdjList;
import com.alibaba.graphscope.ds.adaptor.Nbr;
import com.alibaba.graphscope.fragment.IFragment;
import com.alibaba.graphscope.parallel.ParallelEngine;
import com.alibaba.graphscope.parallel.ParallelMessageManager;
import com.alibaba.graphscope.parallel.message.DoubleMsg;
import com.alibaba.graphscope.utils.FFITypeFactoryhelper;
import org.slf4j.Logger;
import org.slf4j.LoggerFactory;
import java.util.function.BiConsumer;
import java.util.function.Supplier;
public class PageRank extends Communicator
implements ParallelAppBase<Long, Long, Long, Double, PageRankContext>, ParallelEngine {
private static Logger logger = LoggerFactory.getLogger(PageRank.class);
@Override
public void PEval(
IFragment<Long, Long, Long, Double> fragment,
ParallelContextBase<Long, Long, Long, Double> contextBase,
ParallelMessageManager parallelMessageManager) {
PageRankContext ctx = (PageRankContext) contextBase;
parallelMessageManager.initChannels(ctx.thread_num());
VertexRange<Long> innerVertices = fragment.innerVertices();
int totalVertexNum = (int) fragment.getTotalVerticesNum();
ctx.superStep = 0;
double base = 1.0 / totalVertexNum;
BiConsumer<Vertex<Long>, Integer> calc =
(Vertex<Long> vertex, Integer finalTid) -> {
int edgeNum = (int) fragment.getOutgoingAdjList(vertex).size();
ctx.degree.set(vertex, edgeNum);
if (edgeNum == 0) {
ctx.pagerank.set(vertex, base);
} else {
ctx.pagerank.set(vertex, base / edgeNum);
DoubleMsg msg = FFITypeFactoryhelper.newDoubleMsg(base / edgeNum);
parallelMessageManager.sendMsgThroughOEdges(
fragment, vertex, msg, finalTid);
}
};
forEachVertex(innerVertices, ctx.thread_num, ctx.executor, calc);
int innerVertexSize = (int) fragment.getInnerVerticesNum();
for (int i = 0; i < innerVertexSize; ++i) {
if (ctx.degree.get(i) == 0) {
ctx.danglingVNum += 1;
}
}
DoubleMsg msgDanglingSum = FFITypeFactoryhelper.newDoubleMsg(0.0);
DoubleMsg localSumMsg = FFITypeFactoryhelper.newDoubleMsg(base * ctx.danglingVNum);
sum(localSumMsg, msgDanglingSum);
ctx.danglingSum = msgDanglingSum.getData();
parallelMessageManager.forceContinue();
}
@Override
public void IncEval(
IFragment<Long, Long, Long, Double> fragment,
ParallelContextBase<Long, Long, Long, Double> contextBase,
ParallelMessageManager parallelMessageManager) {
PageRankContext ctx = (PageRankContext) contextBase;
int innerVertexNum = (int) fragment.getInnerVerticesNum();
VertexRange<Long> innerVertices = fragment.innerVertices();
ctx.superStep = ctx.superStep + 1;
if (ctx.superStep > ctx.maxIteration) {
for (int i = 0; i < innerVertexNum; ++i) {
if (ctx.degree.get(i) != 0) {
ctx.pagerank.set(i, ctx.degree.get(i) * ctx.pagerank.get(i));
}
}
ctx.executor.shutdown();
return;
}
int totalVertexNum = (int) fragment.getTotalVerticesNum();
double base = (1.0 - ctx.alpha) / totalVertexNum + ctx.alpha * ctx.danglingSum / totalVertexNum;
BiConsumer<Vertex<Long>, DoubleMsg> consumer =
((vertex, aDouble) -> {
ctx.pagerank.set(vertex, aDouble.getData());
});
Supplier<DoubleMsg> msgSupplier = () -> DoubleMsg.factory.create();
parallelMessageManager.parallelProcess(fragment, ctx.thread_num, ctx.executor, msgSupplier, consumer);
BiConsumer<Vertex<Long>, Integer> calc =
((vertex, finalTid) -> {
if (ctx.degree.get(vertex) == 0) {
ctx.nextResult.set(vertex, base);
} else {
double cur = 0.0;
AdjList<Long, Double> nbrs = fragment.getIncomingAdjList(vertex);
for (Nbr<Long, Double> nbr : nbrs.iterable()) {
cur += ctx.pagerank.get(nbr.neighbor());
}
cur = (cur * ctx.alpha + base) / ctx.degree.get(vertex);
ctx.nextResult.set(vertex, cur);
DoubleMsg msg =
FFITypeFactoryhelper.newDoubleMsg(ctx.nextResult.get(vertex));
parallelMessageManager.sendMsgThroughOEdges(
fragment, vertex, msg, finalTid);
}
});
forEachVertex(innerVertices, ctx.thread_num, ctx.executor, calc);
BiConsumer<Vertex<Long>, Integer> consumer2 =
((vertex, integer) -> {
ctx.pagerank.set(vertex, ctx.nextResult.get(vertex));
});
forEachVertex(innerVertices, ctx.thread_num, ctx.executor, consumer2);
DoubleMsg msgDanglingSum = FFITypeFactoryhelper.newDoubleMsg(0.0);
DoubleMsg localSumMsg = FFITypeFactoryhelper.newDoubleMsg(base * ctx.danglingVNum);
sum(localSumMsg, msgDanglingSum);
ctx.danglingSum = msgDanglingSum.getData();
parallelMessageManager.forceContinue();
}
}
详细说明如下:
-
PEval
在算法初始化阶段,PEval 方法负责执行一系列初始化任务,包括获取全部内部点列表innerVertices,获取全图点的总数totalVertexNum,初始化消息管理对象parallelMessageManager,初始化 pagerank 基准值base等,通过公式 base= 1.0 / totalVertexNum,使所有点都有相同的 pagerank 值,并且总和为 1。PEval 中定义了一个
BiConsumer数据类型的变量,类似于函数对象,这个函数接收两个参数vertex(点)和finalTid(线程 ID)。在后续的forEachVertex遍历点列表时,对每个点调用BiConsumer中包含的函数。这个函数具体的逻辑是:- 获取
vertex(点)的出度并保存到ctx.degree中。其中,ctx.degree是一个 IntArrayWrapper 类型的成员,在 Context 类中定义,用于保存所有内部点的出度信息,初始化的值是 0。 - 如果
vertex(点)的出度是 0(悬挂点,即从这个点出发不会访问到其他点),则将其 pagerank 值设置为基准值base。如果出度不是 0,则按照公式 Pagerank = base / Degree 计算这个点的 pagerank 值,可以看出,出度越多其走到特定点的概率就越小,其 pagerank 值自然就会变小。然后通过sendMsgThroughOEdges将这个点的 pagerank 值沿着出边的方向发送给相应的点。
之后,PEval 将统计当前 Fragment 中悬挂点的数量,并汇总到
ctx.danglingSum,在后续计算 pagerank 值时会使用该数值。可以通过Communicator中的sum方法汇总所有子图的某个变量的值,具体请参考sum方法的说明。最后,PEval 会调用
forceContinue()方法,以保证能触发 IncEval 的执行。 - 获取
-
IncEval
每一次超步迭代都会遍历所有的内部点,大致的计算逻辑是:每个点的当前 pagerank 值按照出度数 N 平均分成 N 份传递到出边的相邻点,即每个点的 pagerank 值等于其所有入边的相邻点的 pagerank 值的和。这个 pagerank 值还需要根据alpha参数和悬挂点的比例进行调整修正。一个点的重要程度与链接到它的点的重要程度有关。 具体的代码过程如下:- 算法终止条件与结果计算
在每次 IncEval 迭代开始时,IncEval 首先会判断当前迭代数是否已经达到算法参数maxIteration给定的最大迭代数。如果达到,则计算最终结果并结束算法。最终结果的计算就是再次计算每个内部点的 pagerank 值,对于出度不为 0 的点,计算公式为:Pagerank = Degree * Pagerank。 - 初始化
base值
PEval 在计算 pagerank 的时候会除以degree,而最终的结果又会乘回来,如果没有其他计算,最终的 pagerank 值就是base。而在 IncEval 的迭代过程中,IncEval 每一次迭代都会重新定义base值,计算公式为:base = (1.0 - alpha + alpha * danglingSum) / totalVertexNum。其中,alpha是算法的参数,表示沿着当前点继续遍历的概率;1-alpha则是跳走的概率;danglingSum表示全图当前已知的悬挂点的比例。 - 接收消息
IncEval 会通过parallelMessageManager.parallelProcess并发处理接收到的消息,这是一个异步的过程,会创建若干线程去执行BiConsumer定义的函数,该函数有vertex(点) 和aDouble(该点对应的pagerank值)两个参数,请注意,PEval 发送的消息也是这两个值。当接收到消息后,会设置这个点在本地的 pagerank 值。 - 计算 pagerank 并发送消息
forEachVertex 遍历内部点列表时,每个点会执行BiConsumer类型的calc定义的函数。此处对每个点的 pagerank 的计算过程与 PEval 中不同,具体步骤如下:- 获取点的所有��入边列表。
- 汇总所有入边相邻点的 pagerank 值到变量
cur。 - 修正当前点的 pagerank 值,计算公式为:cur = (cur * alpha + base) / degree,该值后续会被当做 pagerank 值。请注意,此时修正后的
cur值还不能更新到 pagerank 成员中,因为当前的 pagerank 值还需要参与其他点的计算,所以当前点的 pagerank 值暂时保存在nextResult中。 - 通过
sendMsgThroughOEdges把当前点的cur值传递给其他子图,收到这个消息的子图会将这个值保存为点的 pagerank 值。
- 更新 pagerank
在所有内部点的 pagerank 值计算完成后,统一将这些点的 pagerank 值从nextResult更新到 pagerank 中。 - 汇总 danglingSum
通过sum汇总全图的悬挂点比例,并调用forceContinue()继续下次超步迭代。最后还需要调用parallelMessageManager.forceContinue(),才能继续下一个超步,否则 Worker 会因为没有待发送的消息而认为算法可以结束。而这个算法的结束条件是超步数达到参数maxIteration指定的迭代数量。
- 算法终止条件与结果计算
Python 图算法开发
ArcGraph 图数据库支持用户根据实际情况以 Python 语言开发和运行图算法。
环境准备
请确保已经成功部署 ArcGraph 图数据库中的 ArcGraph OLAP 引擎。图算法的开发与运行应直接在 ArcGraph OLAP 引�擎内进行,无需额外配置 Python 或其他外部环境。
核心 API 概述
MessageStrategy 类
MessageStrategy 类是用于定义消息传递策略的基础类。
kAlongOutgoingEdgeToOuterVertex:对于每个内部点,沿着出边向目标点发送消息。kAlongIncomingEdgeToOuterVertex:对于每个内部点,沿着入边向目标点发送消息。kAlongEdgeToOuterVertex:对于每个内部点,沿着传入和传出边向目标点发送消息。kSyncOnOuterVertex:对于每个外部点,向它所属的子图发送消息(将消息同步到它本身)。
Vertex 类
Vertex 类代表图中的一个点,每个点可以存储属性等信息。
Vertex():在图中创建一个新的点。
VertexRange 类
VertexRange 类表示图中点的范围列表。
VertexRange():点的范围列表,仅包含点 id。begin() → Vertex:返回点范围列表的起始地址。end() → Vertex:返回点范围列表的结束地址。size() → int:返回点范围列表中点的数量。
VertexArray[T] 类
VertexArray[T] 类是一个泛型容器,用于存储与点相关的数据。
VertexArray():点的列表,包含点数据。Init(range: VertexRange):使用默认值初始化VertexArray。Init(range: VertexRange, const T& value):使用指定值初始化VertexArray。operator(v: Vertex) → T:返回点的数据。
Nbr 类
Nbr()neighbor() → Vertex:获取邻居顶点。get_str(column: int) → str:按列 ID 获取边的字符串类型数据。get_int(column: int) → str:按列 ID 获取边的整数类型数据。get_double(column: int) → str:按列 ID 获取边的双精度浮点型数据。
AdjList 类
AdjList()begin() → Nbr:返回邻边列表的起始地址。end() → Nbr:返回邻边列表的结束地址。size() → int:返回邻边列表中边的数量。
Fragment 类
Fragment 类表示图中的一个子图,提供了丰富的接口以访问和操作子图的点、边及其属性。
Fragment 类方法如下:
| 方法名 | 说明 |
|---|---|
Fragment() | - |
fid() → int | 获取子图 id。 |
fnum() → int | 获取子图编号。 |
vertex_label_num() → int | 获取点类型编号。 |
edge_label_num() → int | 获取边类型编号。 |
get_total_nodes_num() → size_t | 获取点的总数。 |
get_nodes_num(vertex_label_id: int) → size_t | 根据点类型 id 获取点(内部点+外部点)的总数。 |
get_inner_nodes_num(vertex_label_id: int) → size_t | 根据点类型 id 获取内部点总数。 |
get_outer_nodes_num(vertex_label_id: int) → size_t | 根据点类型 id 获取外部点总数。 |
nodes(vertex_label_id: int) → VertexRange | 根据点类型 id 获取当前子图中点的范围。 |
inner_nodes(vertex_label_id: int) → VertexRange | 根据点类型 id 获取当前子图的内部点范围。 |
outer_nodes(vertex_label_id: int) → VertexRange | 根据点类型 id 获取当前子图的外部点范围。 |
get_node_fid(v: Vertex) → int | 获取点 v 的子图 id。 |
is_inner_node(v: Vertex) → bool | 判断点 v 是否是当前子图的内部点。 |
is_outer_node(v: Vertex) → bool | 判断点 v 是否是当前子图的外部点。 |
get_node(label_id: int, oid: string&, v: Vertex&) → bool | 根据 oid 获取点。如果 oid 对应的点存在于当前子图中,则返回 True,并将对应点数据赋值给 v。 |
get_inner_node(label_id: int, oid: string&, v: Vertex&) → bool | 根据 oid 获取内部点。如果 oid 对应的内部点存在于当前子图中,则返回 True,并将对应点数据赋值给 v。 |
get_outer_node(label_id: int, oid: string&, v: Vertex&) → bool | 根据 oid 获取外部点。如果 oid 对应的外部点存在于当前子图中,则返回 True,并将对应点数据赋值给 v。 |
get_node_id(v: Vertex) → str | 返回点 v 的 oid。 |
get_outgoing_edges(v: Vertex, edge_label_id: int) → AdjList | 根据��点类型,返回点 v 的出边列表的迭代器。 |
get_incoming_edges(v: Vertex, edge_label_id: int) → AdjList | 根据点类型,返回点 v 的入边列表的迭代器。 |
has_child(v: Vertex, edge_label_id: int) → bool | 如果点有指定边类型 id 的子连接,返回 True。 |
has_parent(v: Vertex, edge_label_id: int) → bool | 如果点有指定边类型 id 的父连接,返回 True。 |
get_indegree(v: Vertex, edge_label_id: int) → int | 返回点的指定边类型 id 的入度。 |
get_outdegree(v: Vertex, edge_label_id: int) → int | 返回点的指定边类型 id 的出度。 |
get_str(v: Vertex, vertex_property_id: int) → str | 根据属性 id 返回点的 str 数据。 |
get_int(v: Vertex, vertex_property_id: int) → int | 根据属性 id 返回点的 int 数据。 |
get_double(v: Vertex, vertex_property_id: int) → double | 根据属性 id 返回点的 double 数据。 |
vertex_labels() → vector[str] | 获取点类型列表。 |
edge_labels() → vector[str] | 获取边类型列表。 |
get_vertex_label_by_id(vertex_label_id: int) → str | 根据点类型 id 获取点类型名字。 |
get_vertex_label_id_by_name(vertex_label_name: str) → int | 根据点类型名字获取点类型 id。 |
get_edge_label_by_id(edge_label_id: int) → str | 根据边类型 id 获取边类型名字。 |
get_edge_label_id_by_name(edge_label_name: str) → int | 根据边类型名字获取边类型 id。 |
vertex_properties(vertex_label_id: int) → vector[pair[str, str]] | 根据点类型 id 获取点属性列表。 |
vertex_properties(vertex_label_name: str) → vector[pair[str, str]] | 根据点类型名字获取点属性列表。 |
edge_properties(edge_label_id: int) → vector[pair[str, str]] | 根据边类型 id 获取边属性列表。 |
edge_properties(edge_label_name: str) → vector[pair[str, str]] | 根据边类型名字获取边属性列表。 |
get_vertex_property_id_by_name(vertex_label_name: str, vertex_property_name: str) → int | 根据点类型名字和点属性名字获取点属性 id。 |
get_vertex_property_id_by_name(vertex_label_id: int, vertex_property_name: str) → int | 根据点类型 id 和点属性名字获取点属性 id。 |
get_vertex_property_by_id(vertex_label_name: str, vertex_property_id: int) → str | 根据点类型名字和点属性 id 获取点属性。 |
get_vertex_property_by_id(vertex_label_id: int, vertex_property_id: int) → int | 根据点类型名字和点属性 id 获取点属性。 |
get_edge_property_id_by_name(edge_label_name: str, edge_property_name: str) → int | 根据边类型名字和边属性名字获取边属性 id。 |
get_edge_property_id_by_name(edge_label_id: int, edge_property_name: str) → int | 根据边类型 id 和边属性名字获取边属性 id。 |
get_edge_property_by_id(edge_label_name: str, edge_property_id: int) → str | 根据边类型名字和边属性 id 获取边属性。 |
get_edge_property_by_id(edge_label_id: int, edge_property_id: int) → int | 根据边类型 id 和边属性 id 获取边属性。 |
Context[VD_TYPE, MD_TYPE] 类
Context()superstep() → int:获取当前超步的编号。get_config(key: str) → str:获取指定键(key)的值,如果键不存在,则返回空字符串。init_value(range: VertexRange, value: MD_TYPE, type: PIEAggregateType):使用指定的值和类型聚合器初始化点范围。register_sync_buffer(v_label_id: int, strategy: MessageStrategy):为点设置自动并行消息策略。set_node_value(v: Vertex, value: VD_TYPE):设置点的值。get_node_value(v: Vertex) → VD_TYPE:获取点的值。
PIEAggregateType 类
PIEAggregateType 定义了聚合消息的策略。当消息自动传递后,每个内部点将使用 PIEAggregateType 定义的策略聚合接收的消息。
kMinAggregate:用于获取最小值的聚合器。kMaxAggregate:用于获取最大值的聚合器。kSumAggregate:用于获取累加值的聚合器。kProductAggregate:用于计算价值乘积的聚合器。kOverwriteAggregate:聚合器会存储一个值,该值在后续的聚合操作中会被新值覆盖。请注意,当多个点并发地向此聚合器写入时,其行为可能变得不确定。kTextAppendAggregate:以字符串为值的聚合器,可以不断向其附加文本。
基本框架
在 ArcGraph 图数据库中,Python 自定义算法的实现遵循 PIE 架构。以下是一个基本代码框架示例,该框架通过为算法添加 pie 注解引入 PIE 框架的支持,同时封装了 PIE 框架的底层逻辑,使算法实现仅需关注 Init、PEval 和 IncEval 三个核心方法。
from arcgraph.analytical.udf.decorators import pie
from arcgraph.framework.app import AppAssets
@pie(vd_type="double", md_type="double")
class YourAlgorithm(AppAssets):
@staticmethod
def Init(frag, context):
pass
@staticmethod
def PEval(frag, context):
pass
@staticmethod
def IncEval(frag, context):
pass
应用示例
在 ArcGraph OLAP 引擎中利用 PIE 模式设计并实现单源最短路径(SSSP)算法,代码示例如下:
from arcgraph.analytical.udf.decorators import pie
from arcgraph.framework.app import AppAssets
@pie(vd_type="double", md_type="double")
class SSSP_PIE(AppAssets):
@staticmethod
def Init(frag, context):
v_label_num = frag.vertex_label_num()
for v_label_id in range(v_label_num):
nodes = frag.nodes(v_label_id)
context.init_value(
nodes, v_label_id, 1000000000.0, PIEAggregateType.kMinAggregate
)
context.register_sync_buffer(v_label_id, MessageStrategy.kSyncOnOuterVertex)
@staticmethod
def PEval(frag, context):
src = int(context.get_config(b"src"))
# 等同于C++中的 `Vertex source;`
arcgraph.declare(arcgraph.Vertex, source)
native_source = False
v_label_num = frag.vertex_label_num()
for v_label_id in range(v_label_num):
if frag.get_inner_node(v_label_id, src, source):
native_source = True
break
if native_source:
context.set_node_value(source, 0)
else:
return
e_label_num = frag.edge_label_num()
for e_label_id in range(e_label_num):
edges = frag.get_outgoing_edges(source, e_label_id)
for e in edges:
dst = e.neighbor()
distv = e.get_int(2)
if context.get_node_value(dst) > distv:
context.set_node_value(dst, distv)
@staticmethod
def IncEval(frag, context):
v_label_num = frag.vertex_label_num()
e_label_num = frag.edge_label_num()
for v_label_id in range(v_label_num):
iv = frag.inner_nodes(v_label_id)
for v in iv:
v_dist = context.get_node_value(v)
for e_label_id in range(e_label_num):
es = frag.get_outgoing_edges(v, e_label_id)
for e in es:
u = e.neighbor()
u_dist = v_dist + e.get_int(2)
if context.get_node_value(u) > u_dist:
context.set_node_value(u, u_dist)
if __name__ == "__main__":
if len(sys.argv) == 1:
print(f"not enough argument\n\npackage: build .gar file\ntest: run app")
sys.exit(0)
if sys.argv[1] == "package":
filepath = f"./my_sssp.gar"
Path(filepath).resolve().unlink(missing_ok=True)
MySssp.to_gar(filepath)
algo_info = """
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
from arcgraph.framework.app import not_compatible_for
from arcgraph.framework.app import project_to_simple
from arcgraph.framework.app import app_attrs
__all__ = ["my_sssp"]
@project_to_simple
@not_compatible_for("arrow_property", "dynamic_property")
def my_sssp(graph, maxIteration:int=10):
...
"""
with zipfile.ZipFile(filepath, "a") as zip_ref:
zip_ref.writestr("my_sssp.py", algo_info)
elif sys.argv[1] == "test":
import pytest
pytest.main(f"-s -v ./test/test.py --name my_sssp".split(" "))
else:
print("argument not support")
如代码所示,用户只需在子图上设计和实现顺序算法,而无需考虑分布式环境中的通信和消息传递。在这种情况下,经典的 Dijkstra 算法及其优化版本适用于处理被集群环境有效切分的大型图数据。